LC 10 - Regular Expression Matching

Question

Given an input string s and a pattern p, implement regular expression matching with support for '.' and '*' where:

• '.' Matches any single character.​​​​
• '*' Matches zero or more of the preceding element.

The matching should cover the entire input string (not partial).

Example 1:

Input: s = "aa", p = "a"
Output: false

Explanation: “a” does not match the entire string “aa”.

Example 2:

Input: s = "aa", p = "a*"
Output: true

Explanation: ‘*’ means zero or more of the preceding element, ‘a’. Therefore, by repeating ‘a’ once, it becomes “aa”.

Example 3:

Input: s = "ab", p = ".*"
Output: true

Explanation: “.” means “zero or more () of any character (.)”.

Constraints:

• 1 <= s.length <= 20
• 1 <= p.length <= 20
• s contains only lowercase English letters.
• p contains only lowercase English letters, '.', and '*'.
• It is guaranteed for each appearance of the character '*', there will be a previous valid character to match.

Links

Question here and solution here

Solution

concept

We can use a decision tree for this question and there are a few cases we need to consider:

1. if s[i] == p[j] exactly or p[j] == ".", then we have found a match, this means (i, j) -> (i + 1, j + 1)
2. if we have encounter a *, there are two sub cases:
   1. if we use the * (and precedent char matches), this means that we have found a match by repeating the precedent char, then (i, j) -> (i + 1, j), j remains the same since we could use the *again
   2. if we do not use the *, this means we are skipping the current char and the *, this means (i, j) -> (i, j + 2)

The base case is such that:

1. if both i and j are out of bound, then we fully matched and the answer is True
2. if only j is out of bound from str p, while there are still char in s, then this is False
3. However, if only i is out of bound and there are still char in p, it still could be True since we might have * which we can use it as repeat 0 times, effectively delete all the remaining char in p.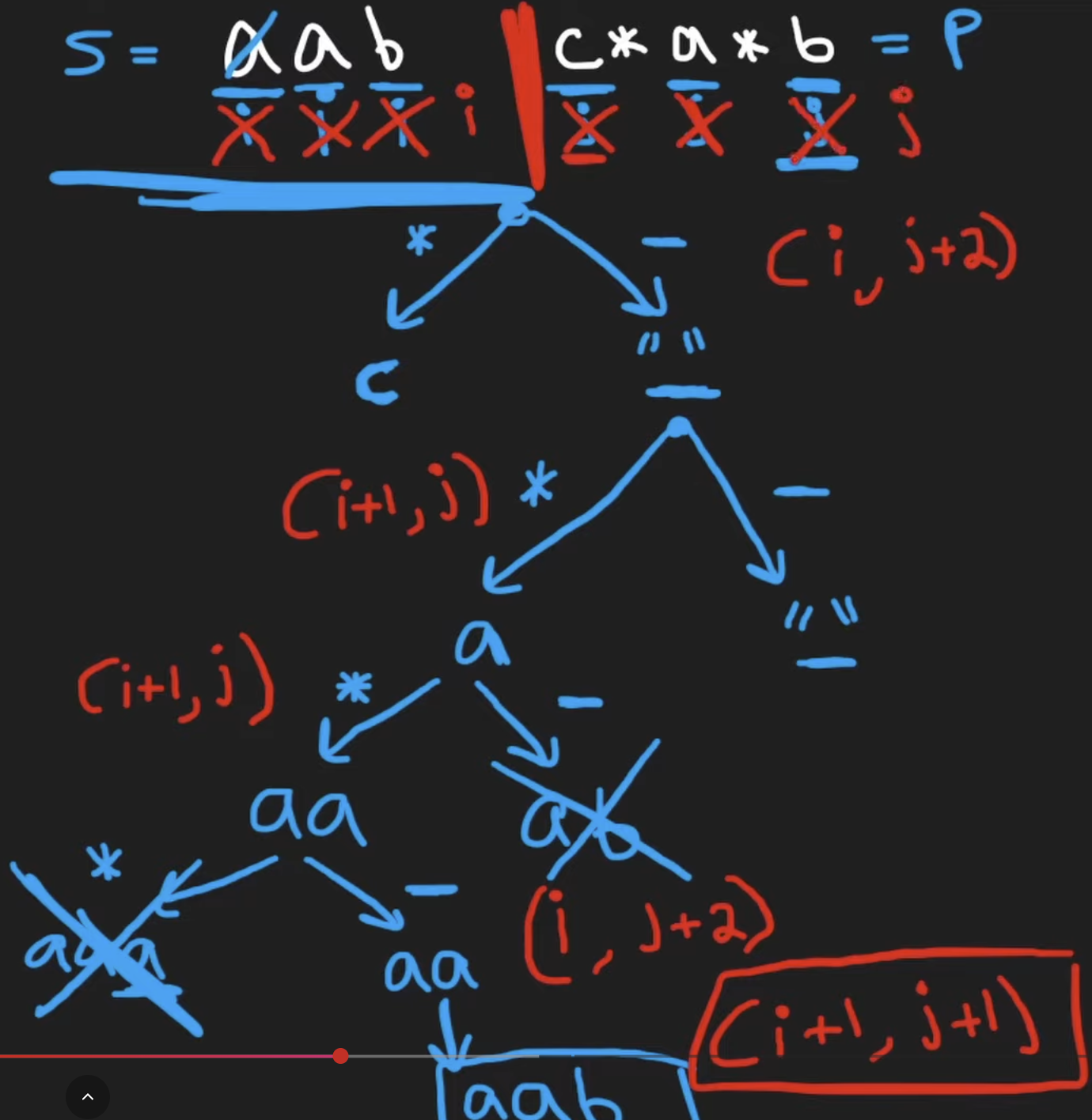

code

class Solution:
	"""
	brute force DFS
	"""
    def isMatch(self, s: str, p: str) -> bool:
        
        def dfs(i,j):
            if i >= len(s) and j >= len(p):
                return True
            if j >= len(p):
                return False

            match = i < len(s) and (s[i] == p[j] or p[j] == ".")

            if (j + 1) < len(p) and p[j + 1] == "*":
                return dfs(i, j + 2) or (match and dfs(i + 1, j)) # dont use * OR use *

            if match:
                return dfs(i + 1, j + 1)

            return False
        
        return dfs(0,0)

class Solution:
	"""
	top down: memoization
	"""
    def isMatch(self, s: str, p: str) -> bool:
        cache = {}
        def dfs(i,j):
            if i >= len(s) and j >= len(p):
                return True
            if j >= len(p):
                return False
            if (i, j) in cache:
                return cache[(i,j)]

            match = i < len(s) and (s[i] == p[j] or p[j] == ".")

            if (j + 1) < len(p) and p[j + 1] == "*":
                cache[(i,j)] = dfs(i, j + 2) or (match and dfs(i + 1, j)) # dont use * OR use *
                return cache[(i,j)]

            if match:
                cache[(i,j)] = dfs(i + 1, j + 1)
                return cache[(i,j)]

            cache[(i,j)] = False
            return cache[(i,j)]
        
        return dfs(0,0)
        
class Solution:
	"""
	bottom up solution
	"""
    def isMatch(self, s: str, p: str) -> bool:
        dp = [[False] * (len(p) + 1) for i in range(len(s) + 1)]
        dp[len(s)][len(p)] = True

        for i in range(len(s), -1, -1):
            for j in range(len(p) - 1, -1, -1):
                match = i < len(s) and (s[i] == p[j] or p[j] == ".")

                if (j + 1) < len(p) and p[j + 1] == "*":
                    dp[i][j] = dp[i][j + 2]
                    if match:
                        dp[i][j] = dp[i + 1][j] or dp[i][j]
                elif match:
                    dp[i][j] = dp[i + 1][j + 1]

        return dp[0][0]

Complexity

time: $O(mn)$
space: $O(mn)$