LC 100 - Same Tree

Question

Given the roots of two binary trees p and q, write a function to check if they are the same or not.

Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.

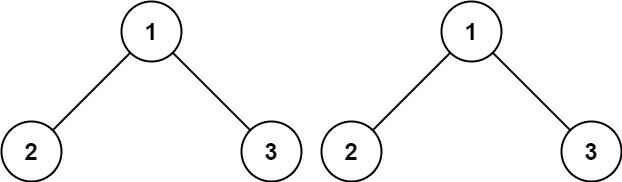
Example 1:

Input: p = [1,2,3], q = [1,2,3]
Output: true

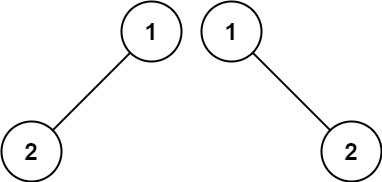
Example 2:

Input: p = [1,2], q = [1,null,2]
Output: false

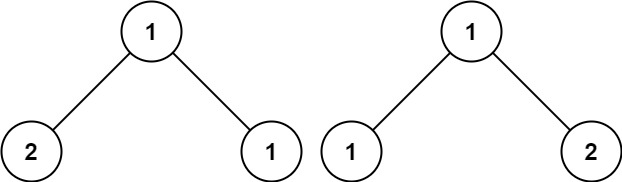
Example 3:

Input: p = [1,2,1], q = [1,1,2]
Output: false

Constraints:

• The number of nodes in both trees is in the range [0, 100].
• -104 <= Node.val <= 104

Links

Question here and solution here

Solution

concept

For DFS solution, we basically check if the current node is the same for both tree and then check the left and right sub tree. For BFS solution, we check level by level.

code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
	"""
	DFS solution
	"""
    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        # if both node is None, then they are the same
        if not p and not q:
            return True
        # if one of the node (but not both) is None, then they are not the same
        elif not p or not q:
            return False
        # if val is diff, immediately return False from the current recursive
        elif p.val != q.val:
            return False

        left_check = self.isSameTree(p.left, q.left)
        right_check = self.isSameTree(p.right, q.right)

        return (left_check and right_check)
        
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
	"""
	BFS solution
	"""
    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        q1 = deque([p])
        q2 = deque([q])

        while q1 and q2:

            for _ in range(len(q1)):
                node_p = q1.popleft()
                node_q = q2.popleft()

                if not node_p and not node_q:
                    continue
                if not node_p or not node_q:
                    return False
                if node_p.val != node_q.val:
                    return False
                
                q1.append(node_p.left)
                q1.append(node_p.right)
                q2.append(node_q.left)
                q2.append(node_q.right)

        return True

Complexity

Time complexity: $O(n)$ Space complexity: $O(h)$

• Best Case (balanced tree): $O(\log(n))$
• Worst Case (degenerate tree): $O(n)$