LC 104 - Maximum Depth of Binary Tree

Question

Given the root of a binary tree, return its maximum depth.

A binary tree’s maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

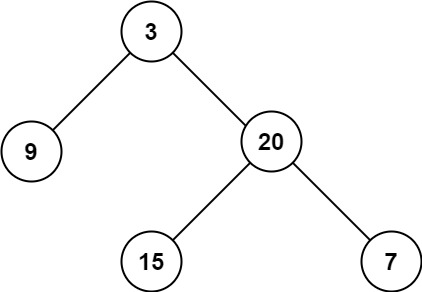
Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

Input: root = [1,null,2]
Output: 2

Constraints:

• The number of nodes in the tree is in the range [0, 104].
• -100 <= Node.val <= 100

Links

Question here and solution here

Solution

concept

There are 3 ways to solve it.

recursive DFS

This is the easiest way, we break down the problem to find the max of the right subtree and left subtree, and return to the parent node with 1 + max(max of right subtree, max of left subtree) to factor in the depth of the current node.

BFS

BFS will need a deque data structure to do level order traversal:

1. we pop from the left the current level node and add their children (if not null) from the right.
2. we need a for loop with range(len(q)) to take snap shot of the current level’s node (so we know how much to traversal in the deque in order to precisely cover the current level, since we will be adding next level’s node from the right at the same time so the deque gets longer)

iterative DFS

Preorder DFS is the easiest to implement iterative DFS. We need a stack data structure to keep track [(node.val, depth)]. We just pop the current node and add in its children along with current depth + 1. As we pop all the nodes within the stack, we keep track the max depth so far.

code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
	"""
	recursive DFS
	"""
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        
        left_max = self.maxDepth(root.left)
        right_max = self.maxDepth(root.right)

        return 1 + max(left_max, right_max)
        
class Solution:
	"""
	BFS
	"""
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        
        depth = 0
        q = deque([root])

        while q:
            for i in range(len(q)):
                node = q.popleft()
                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)
            depth += 1
        return depth
        
class Solution:
	"""
	Iterative DFS
	"""
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0

        ans = 0
        stack = [(root, 1)]
        while stack:
            node, depth = stack.pop()
            if node:
                ans = max(ans, depth)
                stack.append([node.left, depth + 1])
                stack.append([node.right, depth + 1])
        
        return ans

Complexity

recursive DFS

Time complexity: $O(n)$ Space complexity: $O(h)$

• Best Case (balanced tree): $O(\log(n))$
• Worst Case (degenerate tree): $O(n)$