LC 110 - Balanced Binary Tree

Question

Given a binary tree, determine if it is height-balanced.

Example 1:

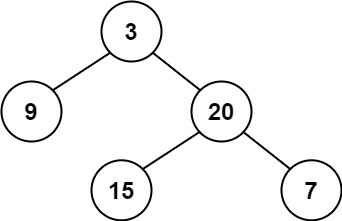
Input: root = [3,9,20,null,null,15,7]
Output: true

Example 2:

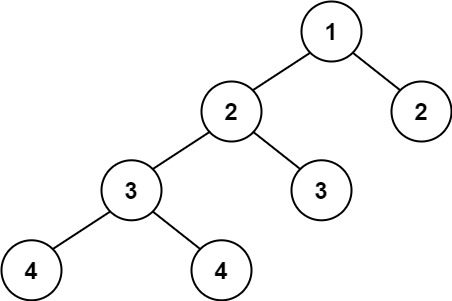
Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

Example 3:

Input: root = []
Output: true

Constraints:

• The number of nodes in the tree is in the range [0, 5000].
• -104 <= Node.val <= 104

Links

Question here and solution here

Solution

concept

We can use the same methods [[543. Diameter of Binary Tree]] and [[104. Maximum Depth of Binary Tree]] to get the height of the right and left sub tree and check if the height difference satisfies the conditions

Note that in NeetCode’s solution, it does not use a global variable self.balanced but instead return together with the height. He update it with left[0] and right[0] and abs(left[1] - right[1]) <= 1 such that if any of the sub tree is not balanced, this information gets propagated up (once one of the sub tree is false, all the way up it will be false).

code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        self.balanced = True

        def dfs(curr):
            if not curr:
                return 0

            h_left = dfs(curr.left)
            h_right = dfs(curr.right)

            if abs(h_left - h_right) > 1:
                self.balanced = False

            return 1 + max(h_left, h_right)

        dfs(root)
        return self.balanced
        
class Solution:
    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        def dfs(root):
            if not root:
                return [True, 0]

            left, right = dfs(root.left), dfs(root.right)
            balanced = left[0] and right[0] and abs(left[1] - right[1]) <= 1
            return [balanced, 1 + max(left[1], right[1])]

        return dfs(root)[0]

Complexity

Time complexity: $O(n)$ Space complexity: $O(h)$

• Best Case (balanced tree): $O(\log(n))$
• Worst Case (degenerate tree): $O(n)$