LC 133 - Clone Graph

Question

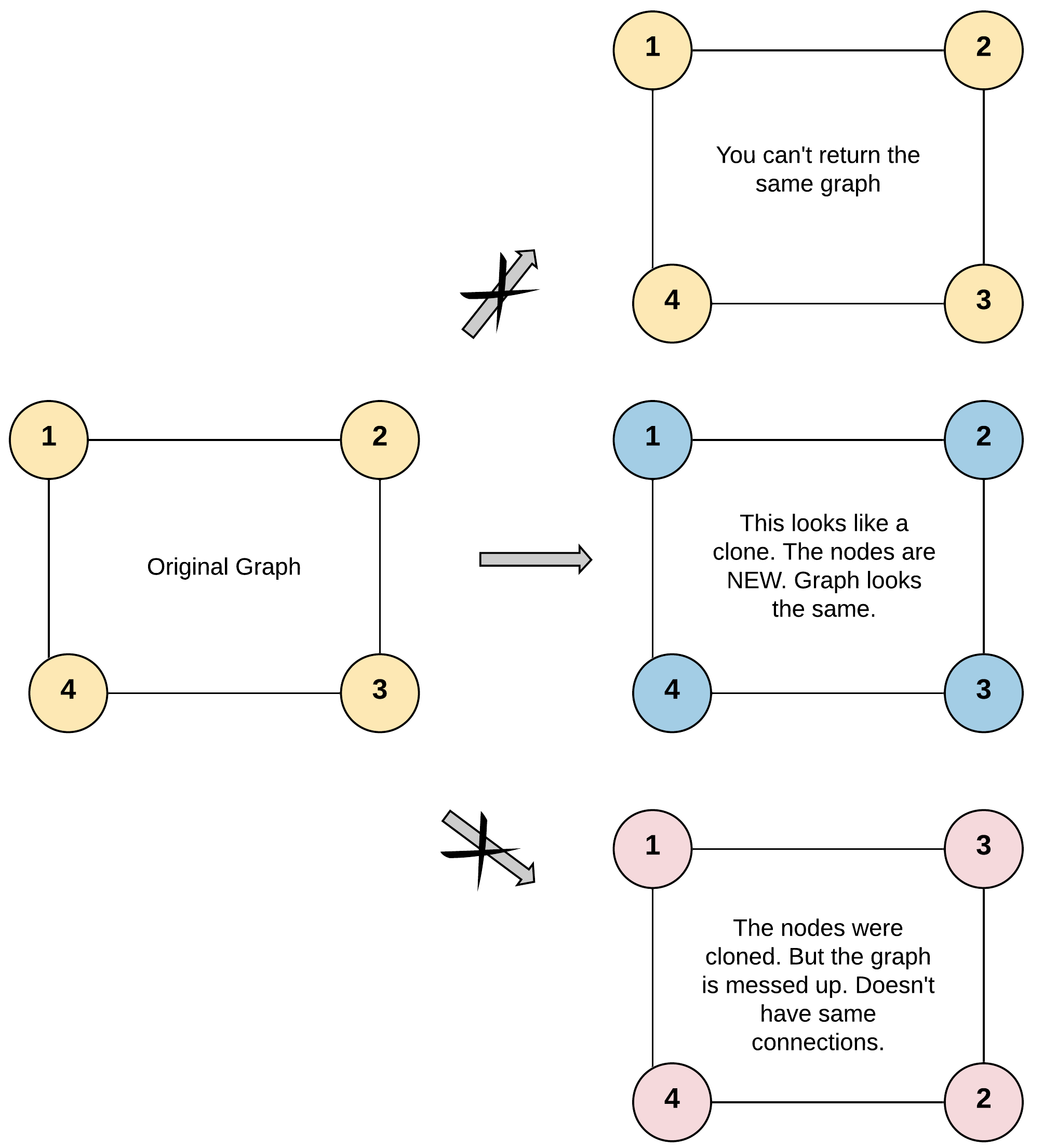
Given a reference of a node in a connected undirected graph.

Return a deep copy (clone) of the graph.

Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.

class Node {
    public int val;
    public List<Node> neighbors;
}

Test case format:

For simplicity, each node’s value is the same as the node’s index (1-indexed). For example, the first node with val == 1, the second node with val == 2, and so on. The graph is represented in the test case using an adjacency list.

An adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.

The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.

Example 1:

Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]

Explanation: There are 4 nodes in the graph. 1st node (val = 1)’s neighbors are 2nd node (val = 2) and 4th node (val = 4). 2nd node (val = 2)’s neighbors are 1st node (val = 1) and 3rd node (val = 3). 3rd node (val = 3)’s neighbors are 2nd node (val = 2) and 4th node (val = 4). 4th node (val = 4)’s neighbors are 1st node (val = 1) and 3rd node (val = 3).

Example 2:

Input: adjList = [[]]
Output: [[]] **Explanation:** Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.

Example 3:

Input: adjList = []
Output: [] **Explanation:** This an empty graph, it does not have any nodes.

Constraints:

• The number of nodes in the graph is in the range [0, 100].
• 1 <= Node.val <= 100
• Node.val is unique for each node.
• There are no repeated edges and no self-loops in the graph.
• The Graph is connected and all nodes can be visited starting from the given node.

Links

Question here and solution here

Solution

concept

Use a hashmap to keep track the mapping from old node to new node. This hashmap has 2 purposes: 1) check if a node has been cloned in $O(1)$ 2) if cloned, we can retrieve and return the cloned node directly in $O(1)$ Please note the Python stores reference (pointer) and not snapshot, so old_to_new[node] = copy both points to the same address of the node, if we modify the node, all calling to the node can reflect that.

code

"""
# Definition for a Node.
class Node:
    def __init__(self, val = 0, neighbors = None):
        self.val = val
        self.neighbors = neighbors if neighbors is not None else []
"""

from typing import Optional
class Solution:
	"""
	DFS solution
	"""
    def cloneGraph(self, node: Optional['Node']) -> Optional['Node']:
        old_to_new = {} # old node to new node
        
        def dfs(node):
            if node in old_to_new:
                return old_to_new[node]
            
            copy = Node() # the starting point
            copy.val = node.val
            old_to_new[node] = copy # we store the pointer to the incomplete node first
            for nei in node.neighbors:
                copy.neighbors.append(dfs(nei))

            return copy

        return dfs(node) if node else None

class Solution:
	"""
	BFS solution
	"""
    def cloneGraph(self, node: Optional['Node']) -> Optional['Node']:
        old_to_new = {} # old node to new node
        
        def bfs(node):
            copy = Node(node.val) # the starting point
            old_to_new[node] = copy
            q = deque([node])

            while q:
                old_curr = q.popleft()
                for nei in old_curr.neighbors:
                    if nei not in old_to_new:
                        old_to_new[nei] = Node(nei.val)
                        q.append(nei)
                    old_to_new[old_curr].neighbors.append(old_to_new[nei])
                
            return copy

        return bfs(node) if node else None  
        
class NeetSolution:
	"""
	DFS
	"""
    def cloneGraph(self, node: Optional['Node']) -> Optional['Node']:
        oldToNew = {}

        def dfs(node):
            if node in oldToNew:
                return oldToNew[node]

            copy = Node(node.val)
            oldToNew[node] = copy
            for nei in node.neighbors:
                copy.neighbors.append(dfs(nei))
            return copy

        return dfs(node) if node else None
        
class NeetSolution:
	"""
	BFS
	"""
    def cloneGraph(self, node: Optional['Node']) -> Optional['Node']:
        if not node:
            return None

        oldToNew = {}
        oldToNew[node] = Node(node.val)
        q = deque([node])

        while q:
            cur = q.popleft()
            for nei in cur.neighbors:
                if nei not in oldToNew:
                    oldToNew[nei] = Node(nei.val)
                    q.append(nei)
                oldToNew[cur].neighbors.append(oldToNew[nei])

        return oldToNew[node]

Complexity

time: $O(n)$ where $n$ is number of nodes + edges.
space: $O(n)$