LC 1448 - Count Good Nodes in Binary Tree

Question

Given a binary tree root, a node X in the tree is named good if in the path from root to X there are no nodes with a value greater than X.

Return the number of good nodes in the binary tree.

Example 1:

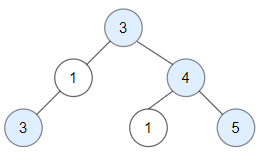
Input: root = [3,1,4,3,null,1,5]
Output: 4

Explanation: Nodes in blue are good. Root Node (3) is always a good node. Node 4 -> (3,4) is the maximum value in the path starting from the root. Node 5 -> (3,4,5) is the maximum value in the path Node 3 -> (3,1,3) is the maximum value in the path.

Example 2:

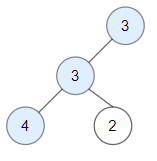
Input: root = [3,3,null,4,2]
Output: 3 **Explanation:** Node 2 -> (3, 3, 2) is not good, because "3" is higher than it.

Example 3:

Input: root = [1]
Output: 1

Explanation: Root is considered as good.

Constraints:

• The number of nodes in the binary tree is in the range [1, 10^5].
• Each node’s value is between [-10^4, 10^4].

Links

Question here and solution here

Solution

concept

Use a Preorder DFS to traverse the tree, we keep track:

1. the max value so far in the path, this max value is evaluated at each node first (preorder)
2. calculate the number of good nodes from left and right on the fly for each node, and return this value at each node

code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def goodNodes(self, root: TreeNode) -> int:

        def dfs(curr, maxVal):
            if not curr:
                return 0

            ans = 1 if curr.val >= maxVal else 0
            maxVal = max(curr.val, maxVal)
            ans += dfs(curr.left, maxVal)
            ans += dfs(curr.right, maxVal)

            return ans
        
        return dfs(root, root.val)
        
class Solution:
    def goodNodes(self, root: TreeNode) -> int:
        self.ans = 0

        def dfs(cur, cur_max):
            if not cur:
                return
            if cur.val >= cur_max:
                self.ans += 1
            
            cur_max = max(cur_max, cur.val)
            dfs(cur.left, cur_max)
            dfs(cur.right, cur_max)
            return

        dfs(root, float("-inf"))
        return self.ans

Complexity

time: $O(n)$
space: $O(n)$