LC 152 - Maximum Product Subarray

Question

Given an integer array nums, find a subarray that has the largest product, and return the product.

The test cases are generated so that the answer will fit in a 32-bit integer.

Example 1:

Input: nums = [2,3,-2,4]
Output: 6

Explanation: [2,3] has the largest product 6.

Example 2:

Input: nums = [-2,0,-1]
Output: 0

Explanation: The result cannot be 2, because [-2,-1] is not a subarray.

Constraints:

• 1 <= nums.length <= 2 * 104
• -10 <= nums[i] <= 10
• The product of any subarray of nums is guaranteed to fit in a 32-bit integer.

Links

Question here and solution here

Solution

concept

suffix and prefix solution

We calculate the suffix and prefix product array but we need to take note that since 0 will reset the array, we have to make the prefix/suffix array reset to nums[i] as well if we encounter a zero. From there we simply compare suffix and prefix array at each position to get the answer I think the main idea is that you cannot have a subarray that do not start at index 0 and -1, it has touch one of the side (except the center one is zero like the one they give in the example).

DP solution

The main trick here is to keep track both max and min such that we can handle upcoming either positive or negative values.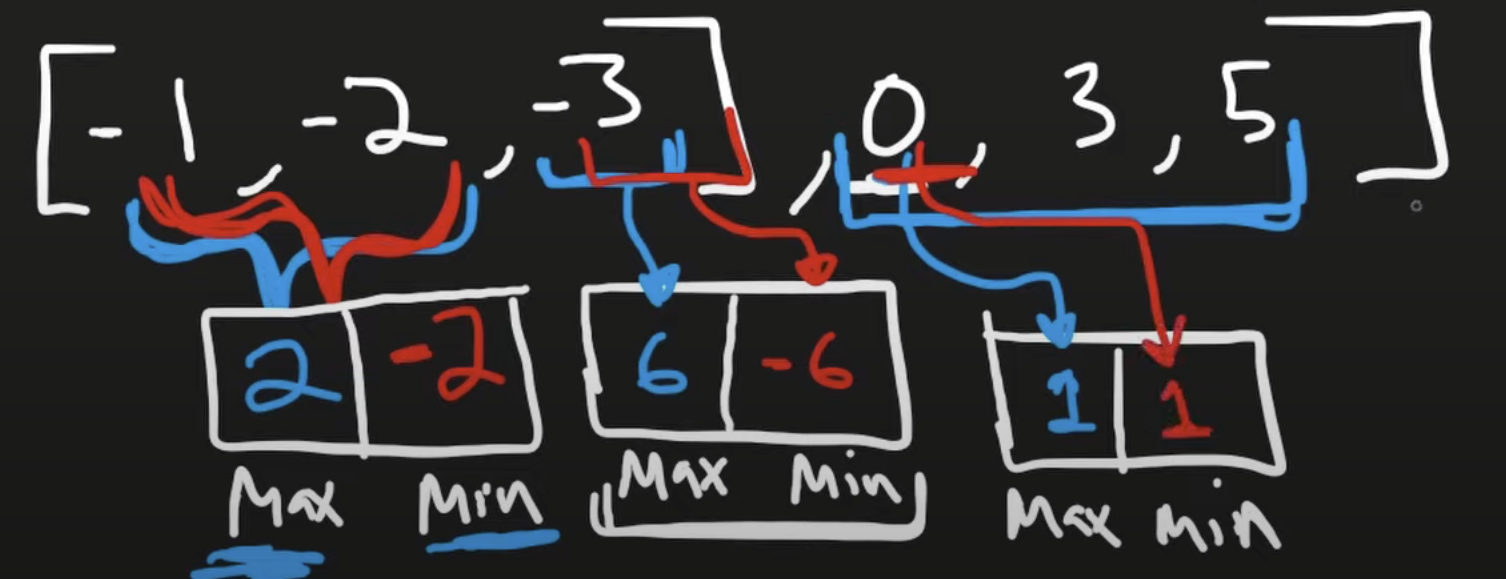

code

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        prefix = [0] * len(nums)
        suffix = [0] * len(nums)

        # need to reset prefix if encounter a 0
        for i in range(len(nums)):
            if i == 0 or prefix[i - 1] == 0: # first term evaluate first
                prefix[i] = nums[i]
                continue
            prefix[i] = prefix[i-1] * nums[i]

        for i in range(len(nums) - 1, -1, -1):
            if i == len(nums) - 1 or prefix[i + 1] == 0:
                suffix[i] = nums[i]
                continue
            suffix[i] = suffix[i + 1] * nums[i]

        ans = float("-inf")
        for i in range(len(nums)):
            ans = max(ans, max(prefix[i], suffix[i]))

        return ans
        
class Solution:
	"""
	DP solution
	Kadane
	"""
    def maxProduct(self, nums: List[int]) -> int:
        ans = float("-inf")
        cur_max, cur_min = 1, 1

        for n in nums:
            tmp = cur_max # store first since we will change this value later, but we need the old cur_max
            cur_max = max(n * cur_max, n * cur_min, n) # (if n is positive, if n is negative, if the case like [-1, 8] where we process 8, 8 itself is the biggest)
            cur_min = min(n * tmp, n * cur_min, n)
            ans = max(ans, cur_max)

        return ans

class Solution:
	"""
	DP solution
	kadane
	"""
    def maxProduct(self, nums: List[int]) -> int:
        ans = max(nums)
        cur_max, cur_min = 1, 1

        for n in nums:
            if n == 0:
                cur_max, cur_min = 1, 1
            tmp = cur_max
            cur_max = max(n*cur_max, n*cur_min, n) # [-1, 8] in this case we want just want n = 8
            cur_min = min(n*tmp, n*cur_min, n) # [-1, -8] in this case we also just want n = -8
            ans = max(ans, cur_max)
        return ans            

Complexity

time: $O(n)$
space: $O(1)$