LC 1584 - Min Cost to Connect All Points

Question

You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].

The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.

Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.

Example 1:

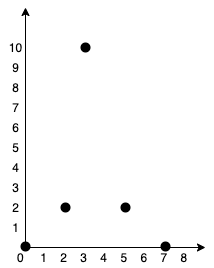
Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
Output: 20

Explanation: We can connect the points as shown above to get the minimum cost of 20. Notice that there is a unique path between every pair of points.

Example 2:

Input: points = [[3,12],[-2,5],[-4,1]]
Output: 18

Constraints:

• 1 <= points.length <= 1000
• -106 <= xi, yi <= 106
• All pairs (xi, yi) are distinct.

Links

Question here and solution here

Solution

concept

This is a Minimum Spanning Tree (MST) which a subset of edges of a connected, weighted, undirected graph that connects all vertices without cycles and with the minimum possible total edge weight -> basically a set of edges that can connects all the nodes (without cycle, i.e. a tree) AND with minimum total edge weight. There are 2 algorithms that can MST from a graph: Prim’s Algorithm and Kruskal’s Algorithm. Usually Prim’s algorithm is more efficient and easier to understand.

Prim’s algorithm is a BFS with greedy approach (with a minimum heap). We start with a node and add its neighbours into the minimum heap. Take note the cost we add into the heap is the distance from the current point to the neighbours and not the accumulate total cost. The accumulative total cost is tracked independently by another variable. This is to make sure we always find the shortest distance from the current point to other point.

Take note here we do not need to record down the source node (the current node that is being processed) into the heap (just the neighbours or the target node) and there could be multiple same node with different distances in the heap. When we pop a node later, we only know that the node is not being visited and has a shorter distance to one of the previously visited node., but this information is enough for us to construct the MST.

Note that Prim’s algorithm is quite similar to Dijkstra’s algorithm as seen in [[743. Network Delay Time]]. There are one key difference:

1. Dijkstra’s algorithm find the minimum distance from a specific point to either the whole map or another specific point (by doing early stop when arrive at that specific point). This means that if there is a branch to the node, the cost (or think of it as time) runs concurrently, like a network delay problem.
2. Prim’s algorithm finds the MST and therefore the cost is the sum of all the edges, the cost here is accumulative from all the branches.
3. This is reflected in the way we store cost/distance/time in the minimum heap

Take note that the starting point of the Prim’s algorithm will determine the shape of the MST, but regardless where we start, the minimum cost will be the same.

code

class Solution:
    def minCostConnectPoints(self, points: List[List[int]]) -> int:
        def calc_dist(p,q):
            x1, y1 = p[0], p[1]
            x2, y2 = q[0], q[1]
            return abs(x1 - x2) + abs(y1 - y2)

        adj_list = defaultdict(list)
        for i in range(len(points)):
            for j in range(len(points)):
                if i == j:
                    continue
                dist = calc_dist(points[i], points[j])
                adj_list[i].append((j, dist))

        visited = set()
        min_heap = [(0, 0)] # weight, node
        cost = 0

        while min_heap:
            weight, node = heapq.heappop(min_heap)
            if node in visited:
                continue

            cost += weight
            visited.add(node)

            for _node, _weight in adj_list[node]:
                if _node not in visited:
                    heapq.heappush(min_heap, (_weight, _node))
            
        return cost
        

class NeetSolution:
    """
    Prim's algorithm
    BFS with min heap
    slightly optimised
    """
    def minCostConnectPoints(self, points: List[List[int]]) -> int:
        # building adjacency list
        N = len(points)
        # i: list of [cost, node]
        adj = {i:[] for i in range(N)}
        for i in range(N):
            x1, y1 = points[i]
            for j in range(i+1, N):
                x2, y2 = points[j]
                cost = abs(x1 - x2) + abs(y1 - y2)
                # since it is undirected, add in both
                adj[i].append([cost, j])
                adj[j].append([cost, i])

        # prim's algo
        result = 0
        visited = set()
        minHeap = [[0,0]]
        while len(visited) < N:
            cost, i = heapq.heappop(minHeap)
            if i in visited:
                continue
            result += cost
            visited.add(i)
            for neighbor_cost, neighbor in adj[i]:
                if neighbor not in visited:
                    heapq.heappush(minHeap, [neighbor_cost, neighbor])
        return result

Complexity

time: $O(n^2 \log n)$
space: $O(n^2)$