LC 2013 - Detect Squares

Question

You are given a stream of points on the X-Y plane. Design an algorithm that:

• Adds new points from the stream into a data structure. Duplicate points are allowed and should be treated as different points.
• Given a query point, counts the number of ways to choose three points from the data structure such that the three points and the query point form an axis-aligned square with positive area.

An axis-aligned square is a square whose edges are all the same length and are either parallel or perpendicular to the x-axis and y-axis.

Implement the DetectSquares class:

• DetectSquares() Initializes the object with an empty data structure.
• void add(int[] point) Adds a new point point = [x, y] to the data structure.
• int count(int[] point) Counts the number of ways to form axis-aligned squares with point point = [x, y] as described above.

Example 1:

Input
["DetectSquares", "add", "add", "add", "count", "count", "add", "count"]
[[], [[3, 10]], [[11, 2]], [[3, 2]], [[11, 10]], [[14, 8]], [[11, 2]], [[11, 10]]]
Output
[null, null, null, null, 1, 0, null, 2]

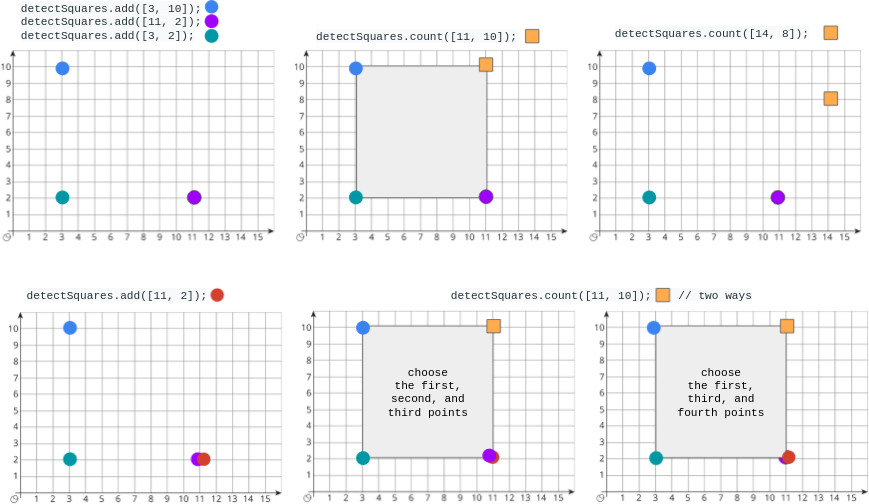
Explanation DetectSquares detectSquares = new DetectSquares(); detectSquares.add([3, 10]); detectSquares.add([11, 2]); detectSquares.add([3, 2]); detectSquares.count([11, 10]); // return 1. You can choose: // - The first, second, and third points detectSquares.count([14, 8]); // return 0. The query point cannot form a square with any points in the data structure. detectSquares.add([11, 2]); // Adding duplicate points is allowed. detectSquares.count([11, 10]); // return 2. You can choose: // - The first, second, and third points // - The first, third, and fourth points

Constraints:

• point.length == 2
• 0 <= x, y <= 1000
• At most 3000 calls in total will be made to add and count.

Links

Question here and solution here

Solution

concept

We can append the points into a list which essentially keep track all the points so far, the reason for this list is because we need to record down duplicate as well. We will also record the count of the points as well.

The key concept for the count method here is to:

1. for every query point, we first go through the list to find the diagonal point
2. if the diagonal point exist, we will then find the other 2 points (that forms the square) and multiply them together. This is because they want number of ways a square can be formed.
3. the duplicates in the list for the diagonal point is also taken care of, in the sense we will go through the point multiple time and each time the corresponding 2 points at the corner will be counted again.

code

class DetectSquares:

    def __init__(self):
        self.pts = [] # keep track the points
        self.pts_count = defaultdict(int)

    def add(self, point: List[int]) -> None:
        self.pts.append(point)
        self.pts_count[tuple(point)] += 1

    def count(self, point: List[int]) -> int:
        ans = 0
        x, y = point
        for _x, _y in self.pts:
            if abs(x - _x) != abs(y - _y) or x == _x or y == _y:
                continue
            ans += self.pts_count[(_x, y)] * self.pts_count[(x, _y)]
        return ans


# Your DetectSquares object will be instantiated and called as such:
# obj = DetectSquares()
# obj.add(point)
# param_2 = obj.count(point)

Complexity

time: $O(n)$
space: $O(n)$