LC 207 - Course Schedule

Question

There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course bi first if you want to take course ai.

• For example, the pair [0, 1], indicates that to take course 0 you have to first take course 1.

Return true if you can finish all courses. Otherwise, return false.

Example 1:

Input: numCourses = 2, prerequisites = [[1,0]]
Output: true **Explanation:** There are a total of 2 courses to take.  To take course 1 you should have finished course 0. So it is possible.

Example 2:

Input: numCourses = 2, prerequisites = [[1,0],[0,1]]
Output: false **Explanation:** There are a total of 2 courses to take.  To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.

Constraints:

• 1 <= numCourses <= 2000
• 0 <= prerequisites.length <= 5000
• prerequisites[i].length == 2
• 0 <= ai, bi < numCourses
• All the pairs prerequisites[i] are unique.

Links

Question here and solution here

Solution

concept

The main concept here is to think of it as a graph. 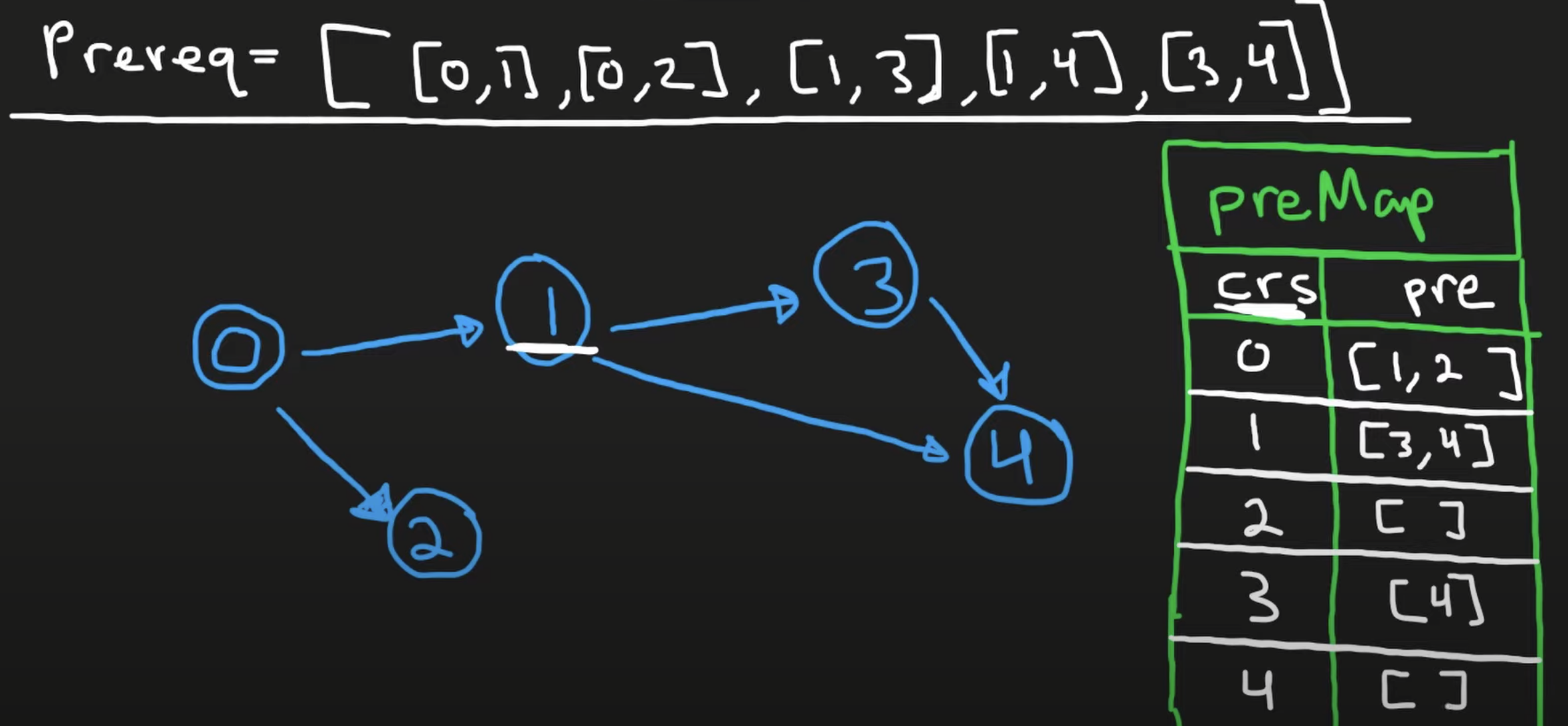We need to keep moving forward in the graph to check for the pre-req of the current course. We keep track a hashmap (or adjacency list) and as long as we detected a cycle, the answer will be false.

Note that this flow is making more sense (although in this case the answer is the same), we can also do pre_req[prereq].append(course) which will make the graph reverse in the sense that it is prereq - > course. But we note that, logically, if A is the prereq of B, if we want to take B we must take A first. But if we took A, it is not a must we have to take B, we can just stop there or take other courses like C, so this chain is abit weaker in the logical sense.

code

class Solution:
    def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
        pre_req = {i : [] for i in range(numCourses)} # {course: [prereq]}
        for course, prereq in prerequisites:
            pre_req[course].append(prereq)
        
        visited = set()
        def dfs(course):
            if course in visited:
                return False
            if pre_req[course] == []:
                return True
            
            visited.add(course)
            for prereq in pre_req[course]:
                if not dfs(prereq): return False
            visited.remove(course)
            pre_req[course] = []
            return True
            
		# need this in case the graph is not totally connected
        for _course in range(numCourses):
            if not dfs(_course): return False

        return True

Complexity

time: $O(V+E)$
space: $O(V+E)$