LC 212 - Word Search II

Question

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Example 1:

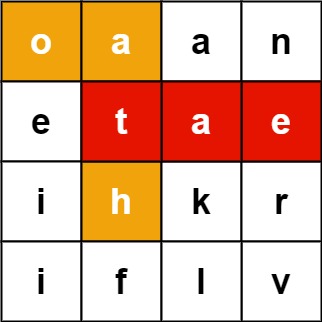
Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]

Example 2:

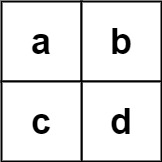
Input: board = [["a","b"],["c","d"]], words = ["abcb"]
Output: []

Constraints:

• m == board.length
• n == board[i].length
• 1 <= m, n <= 12
• board[i][j] is a lowercase English letter.
• 1 <= words.length <= 3 * 104
• 1 <= words[i].length <= 10
• words[i] consists of lowercase English letters.
• All the strings of words are unique.

Links

Question here and solution here

Solution

concept

This question needs Trie + standard DFS to solve.

code

class TrieNode:
    def __init__(self):
        self.children = {}
        self.end_of_word = False

    def add_word(self, word):
        cur = self
        for c in word:
            if c not in cur.children:
                cur.children[c] = TrieNode()
            cur = cur.children[c]
        cur.end_of_word = True

class Solution:
    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
        root = TrieNode()
        for w in words:
            root.add_word(w)
        
        ROWS, COLS = len(board), len(board[0])
        result, visited = set(), set()
        directions = [[0,1], [1,0], [0, -1], [-1, 0]]

        def dfs(r, c, node, word):
            if (r < 0 or r >= ROWS or
                c < 0 or c >= COLS or 
                (r,c) in visited or board[r][c] not in node.children):
                return
            
            visited.add((r, c))
            node = node.children[board[r][c]]
            word += board[r][c]
            if node.end_of_word:
                result.add(word)
            
            for dr, dc in directions:
                dfs(r + dr, c + dc, node, word)

            visited.remove((r,c))

        for r in range(ROWS):
            for c in range(COLS):
                dfs(r,c, root, "")
        
        return list(result)

Complexity

time: $O(m \times n \times 4 \times 3^{t-1} + s)$
space: $O(n)$