LC 235 - Lowest Common Ancestor of a Binary Search Tree

Question

Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1:

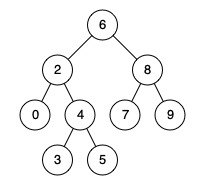
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6

Explanation: The LCA of nodes 2 and 8 is 6.

Example 2:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2

Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Example 3:

Input: root = [2,1], p = 2, q = 1
Output: 2

Constraints:

• The number of nodes in the tree is in the range [2, 105].
• -109 <= Node.val <= 109
• All Node.val are unique.
• p != q
• p and q will exist in the BST.

Links

Question here and solution here

Solution

concept

Making use of the BST properties, if the p and q ‘s value is all smaller than the current node value as we DFS the tree, then we know that both p and q is at the left side of our current node. The same goes for if p and q are both bigger than the current node. if we encounter a situation where

1. p and q are at the different side of the current node OR
2. p or q is the current node then we found our answer.

code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':

        def dfs(curr):
            if not curr:
                return None

            if (p.val <= curr.val <= q.val) or (q.val <= curr.val <= p.val):
                ans = curr
            elif p.val > curr.val and q.val > curr.val: # go to right side
                ans = dfs(curr.right)
            else: # go to the left side
                ans = dfs(curr.left)

            return ans  
            
        return dfs(root)
        
class NeetSolution:
    def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:
        while True:
            if root.val < p.val and root.val < q.val:
                root = root.right
            elif root.val > p.val and root.val > q.val:
                root = root.left
            else:
                return root

Complexity

time: $O(\log n)$ we only has to visit 1 node per level, so its roughly the height of the tree
space: $O(1)$