LC 286 - Walls and Gates

Question

You are given an m x n grid rooms initialized with these three possible values.

• -1 A wall or an obstacle.
• 0 A gate.
• INF Infinity means an empty room. We use the value 231 - 1 = 2147483647 to represent INF as you may assume that the distance to a gate is less than 2147483647.

Fill each empty room with the distance to its nearest gate. If it is impossible to reach a gate, it should be filled with INF.

Example 1:

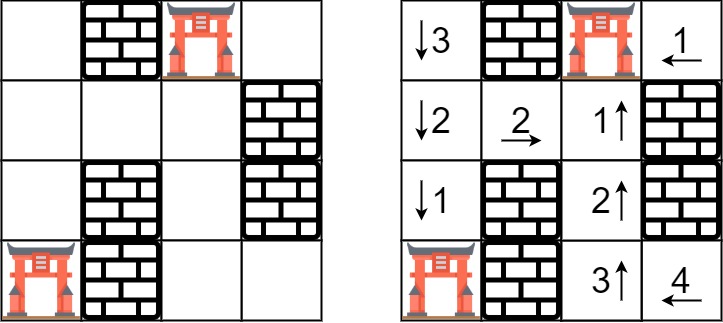
Input: rooms = [[2147483647,-1,0,2147483647],[2147483647,2147483647,2147483647,-1],[2147483647,-1,2147483647,-1],[0,-1,2147483647,2147483647]]
Output: [[3,-1,0,1],[2,2,1,-1],[1,-1,2,-1],[0,-1,3,4]]

Example 2:

Input: rooms = [[-1]]
Output: [[-1]]

Constraints:

• m == rooms.length
• n == rooms[i].length
• 1 <= m, n <= 250
• rooms[i][j] is -1, 0, or 231 - 1.

Links

Question here and solution here

Solution

concept

Since there are multiple gates in the grid and if we do DFS on each cell the time complexity would $O((mn)^2)$. The most optimal solution here is to use a multi-source BFS where the we run BFS from the gate. At each layer we run from the gate together and update the distance. If visited we will not visit again and this implicitly ensure that the that cell’s value (i.e. distance) is the smallest from the nearest gate.

Take note LeetCode’s DFS solution (TLE) where the path is being tracked (in the sense that visited array need to be removed after each dfs call similar to backtracking).

1. for problem that needs to track a path for each run, this is needed as one path might need to visit another path in the same run, if we do not remove it from the visited then the answer will be wrong
2. for problem that simply need to fill-up the graph, there is no need to remove elements from visited.

code

class Solution:
	"""
	multi-source BFS
	"""
    def wallsAndGates(self, rooms: List[List[int]]) -> None:
        """
        Do not return anything, modify rooms in-place instead.
        """
        ROWS, COLS = len(rooms), len(rooms[0])
        visited = set()
        q = deque()
        directions = [[0,1],[1,0],[0,-1],[-1,0]]

        def AddRoom(r,c):
            if (r < 0 or r >= ROWS or
                c < 0 or c >= COLS or
                (r, c) in visited or
                rooms[r][c] == -1):
                return
            
            visited.add((r,c))
            q.append((r,c))

        # add only gate into queue
        for r in range(ROWS):
            for c in range(COLS):
                if rooms[r][c] == 0:
                    q.append((r, c))
                    visited.add((r, c))

        dist = 0
        while q:
            for _ in range(len(q)):
                r, c = q.popleft()
                rooms[r][c] = dist
                for dr, dc in directions:
                    AddRoom(r + dr, c + dc)
            dist += 1
            
class NeetSolution:
	"""
	DFS from each cell
	TLE
	"""
    def wallsAndGates(self, rooms: List[List[int]]) -> None:
        """
        Do not return anything, modify rooms in-place instead.
        """
        ROWS, COLS = len(rooms), len(rooms[0])
        directions = [(1, 0), (-1, 0), (0, 1), (0, -1)]
        INF = 2147483647
        visit = [[False for _ in range(COLS)] for _ in range(ROWS)]

        def dfs(r, c):
            if (r < 0 or c < 0 or r >= ROWS or
                c >= COLS or rooms[r][c] == -1 or
                visit[r][c]):
                return INF
            if rooms[r][c] == 0:
                return 0

            visit[r][c] = True
            res = INF
            for dx, dy in directions:
                res = min(res, 1 + dfs(r + dx, c + dy))
            visit[r][c] = False
            return res

        for r in range(ROWS):
            for c in range(COLS):
                if rooms[r][c] == INF:
                    rooms[r][c] = dfs(r, c)
                    
class NeetSolution:
	"""
	single source BFS from each cell
	TLE
	"""
    def wallsAndGates(self, rooms: List[List[int]]) -> None:
        """
        Do not return anything, modify rooms in-place instead.
        """
        ROWS, COLS = len(rooms), len(rooms[0])
        directions = [(1, 0), (-1, 0), (0, 1), (0, -1)]
        INF = 2147483647

        def bfs(r, c):
            q = deque([(r, c)])
            visit = [[False] * COLS for _ in range(ROWS)]
            visit[r][c] = True
            steps = 0
            while q:
                for _ in range(len(q)):
                    row, col = q.popleft()
                    if rooms[row][col] == 0:
                        return steps
                    for dr, dc in directions:
                        nr, nc = row + dr, col + dc
                        if (0 <= nr < ROWS and 0 <= nc < COLS and
                            not visit[nr][nc] and rooms[nr][nc] != -1
                        ):
                            visit[nr][nc] = True
                            q.append((nr, nc))
                steps += 1
            return INF

        for r in range(ROWS):
            for c in range(COLS):
                if rooms[r][c] == INF:
                    rooms[r][c] = bfs(r, c)

Complexity

time: $O(mn)$
space: $O(mn)$