LC 300 - Longest Increasing Subsequence

Question

Given an integer array nums, return the length of the longest strictly increasing subsequence.

Example 1:

Input: nums = [10,9,2,5,3,7,101,18]
Output: 4

Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.

Example 2:

Input: nums = [0,1,0,3,2,3]
Output: 4

Example 3:

Input: nums = [7,7,7,7,7,7,7]
Output: 1

Constraints:

• 1 <= nums.length <= 2500
• -104 <= nums[i] <= 104

Follow up: Can you come up with an algorithm that runs in O(n log(n)) time complexity?

Links

Question here and solution here

Solution

concept

memoization

We use DFS to scan through index i. The key part is to cache an array where the LIS (from i till end of num, i,e, the behind part of the array) at index i is cached. At each index i, we will run through i+1 till end of nums to get the LIS at that index i. And this is the value we will cache.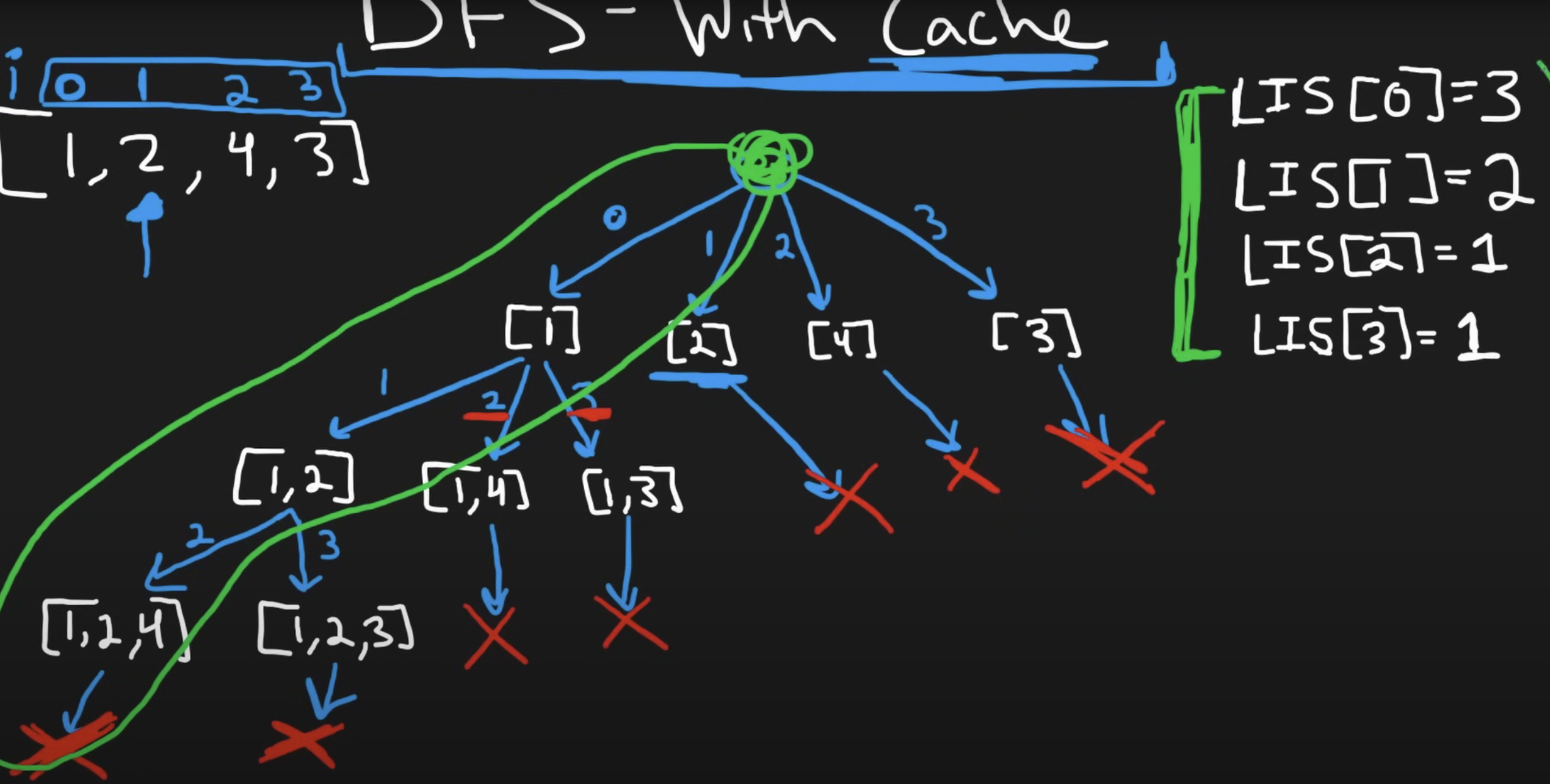

bottom up

We iterate the nums array from reverse, at each index i , we will run check for LIS if the condition of strictly increasing order is met, and if yes we will use the cached value. The sub problem here is to figure out the LIS at each index (LIS from the array from i to end of nums) 1 means itself, which is always true because the number itself is a candidate of LIS.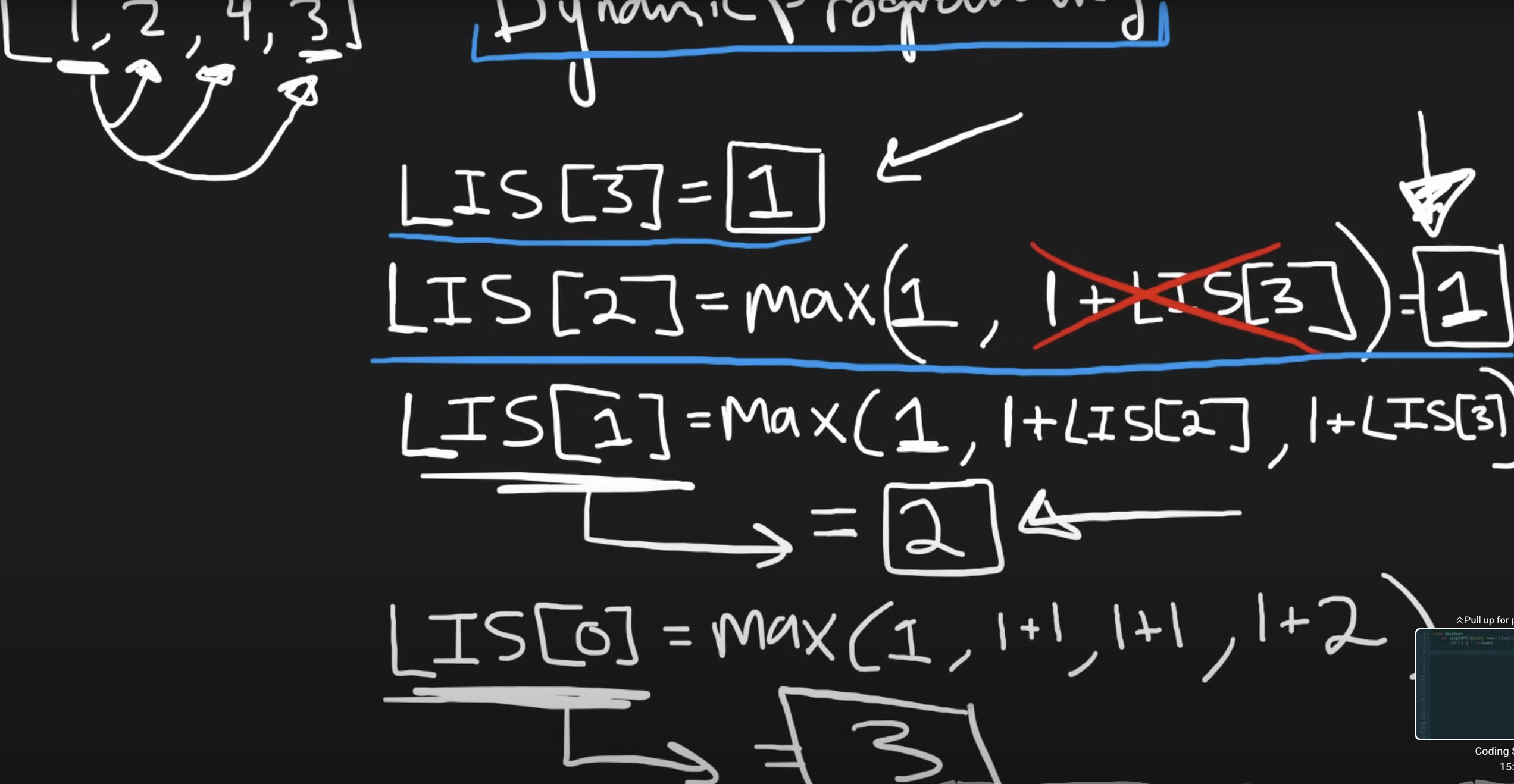

code

class Solution:
	"""
	brute force
	TLE
	"""
    def lengthOfLIS(self, nums: List[int]) -> int:
        
        def dfs(i):
            LIS = 1
            for j in range(i + 1, len(nums)):
                if nums[i] < nums[j]:
                    LIS = max(LIS, 1 + dfs(j))
            return LIS

        return max(dfs(i) for i in range(len(nums)))
        
class Solution:
	"""
	top down: memoization
	"""
    def lengthOfLIS(self, nums: List[int]) -> int:
        cache = [-1] * len(nums) # LIS at index i

        def dfs(i):
            if cache[i] != -1:
                return cache[i]

            LIS = 1
            for j in range(i + 1, len(nums)):
                if nums[i] < nums[j]:
                    LIS = max(LIS, 1 + dfs(j))
            cache[i] = LIS
            return cache[i]

        return max(dfs(i) for i in range(len(nums)))

class Solution:
	"""
	bottom up solution
	"""
    def lengthOfLIS(self, nums: List[int]) -> int:
        dp = [1]*len(nums)

        for i in range(len(nums)-1, -1, -1):
            for j in range(i+1, len(nums)):
                if nums[i] < nums[j]:
                    dp[i] = max(dp[i], 1 + dp[j])
        
        return max(dp)

Complexity

time: $O(n^2)$
space: $O(n)$