LC 309 - Best Time to Buy and Sell Stock with Cooldown

Question

You are given an array prices where prices[i] is the price of a given stock on the ith day.

Find the maximum profit you can achieve. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times) with the following restrictions:

• After you sell your stock, you cannot buy stock on the next day (i.e., cooldown one day).

Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).

Example 1:

Input: prices = [1,2,3,0,2]
Output: 3

Explanation: transactions = [buy, sell, cooldown, buy, sell]

Example 2:

Input: prices = [1]
Output: 0

Constraints:

• 1 <= prices.length <= 5000
• 0 <= prices[i] <= 1000

Links

Question here and solution here

Solution

concept

Notice that at each stage we always have the option to go cooldown. The real decision is the buy or sell option.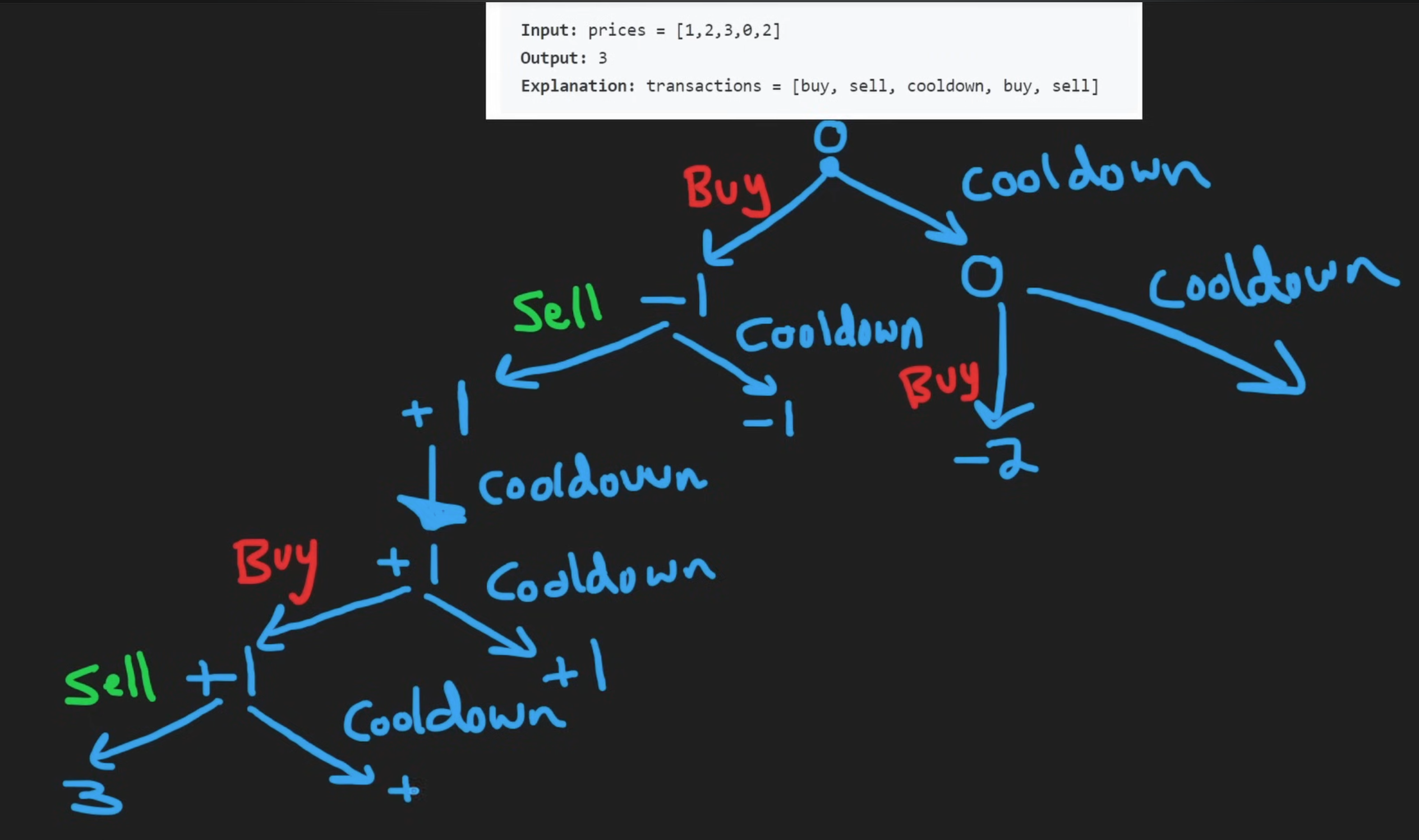

code

class Solution:
	"""
	brute force backtracking
	TLE
	"""
    def maxProfit(self, prices: List[int]) -> int:
        def dfs(i, buying):
            if i >= len(prices):
                return 0
            
            if buying:
                buy = dfs(i + 1, not buying) - prices[i]
                cooldown = dfs(i + 1, buying)
                profit = max(buy, cooldown)
            else:
                sell = dfs(i + 2, not buying) + prices[i]
                cooldown = dfs(i + 1, buying)
                profit = max(sell, cooldown)
            return profit
        
        return dfs(0, True)
        
class Solution:
	"""
	top down: memoization
	"""
    def maxProfit(self, prices: List[int]) -> int:
        cache = {}
        def dfs(i, buying):
            if i >= len(prices):
                return 0
            
            if (i, buying) in cache:
                return cache[(i, buying)]
            
            if buying:
                buy = dfs(i + 1, not buying) - prices[i]
                cooldown = dfs(i + 1, buying)
                profit = max(buy, cooldown)
            else:
                sell = dfs(i + 2, not buying) + prices[i]
                cooldown = dfs(i + 1, buying)
                profit = max(sell, cooldown)
            cache[(i, buying)] = profit
            return cache[(i, buying)]
        
        return dfs(0, True)
        
class Solution:
	"""
	bottom up solution
	"""
    def maxProfit(self, prices: List[int]) -> int:
        n = len(prices)
        dp = [[0] * 2 for _ in range(n + 1)] # [selling, buying]

        for i in range(n - 1, -1, -1):
            for buying in [True, False]:
                if buying:
                    buy = dp[i + 1][False] - prices[i] if i + 1 < n else -prices[i]
                    cooldown = dp[i + 1][True] if i + 1 < n else 0
                    dp[i][1] = max(buy, cooldown)
                else:
                    sell = dp[i + 2][True] + prices[i] if i + 2 < n else prices[i]
                    cooldown = dp[i + 1][False] if i + 1 < n else 0
                    dp[i][0] = max(sell, cooldown)

        return dp[0][1]

Complexity

time: $O(n)$
space: $O(n)$