LC 312 - Burst Balloons
Question
You are given n balloons, indexed from 0 to n - 1. Each balloon is painted with a number on it represented by an array nums. You are asked to burst all the balloons.
If you burst the ith balloon, you will get nums[i - 1] * nums[i] * nums[i + 1] coins. If i - 1 or i + 1 goes out of bounds of the array, then treat it as if there is a balloon with a 1 painted on it.
Return the maximum coins you can collect by bursting the balloons wisely.
Example 1:
1
2
Input: nums = [3,1,5,8]
Output: 167
Explanation: nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> [] coins = 3*1*5 + 3*5*8 + 1*3*8 + 1*8*1 = 167
Example 2:
1
2
Input: nums = [1,5]
Output: 10
Constraints:
n == nums.length1 <= n <= 3000 <= nums[i] <= 100
Links
Question here and solution here
Solution
concept
The key observations here is to actually think about what is a good sub-problem ? Given the nums , if we pop the ith ballon first, the remaining two arrays nums[:i] and nums[1+1:] cannot be calculated independently as the boundaries of the two array should be joined together to be considered. The way to go forward is to consider the case where we pop ith ballon last. This means that the left and right array would be empty already and they are not joint together. We would keep track of l and r pointer to keep track the window (of the sub-array) to be considered, and take note that the i th element is stil being considered, since this element is to be popped last so its effect is still in place. 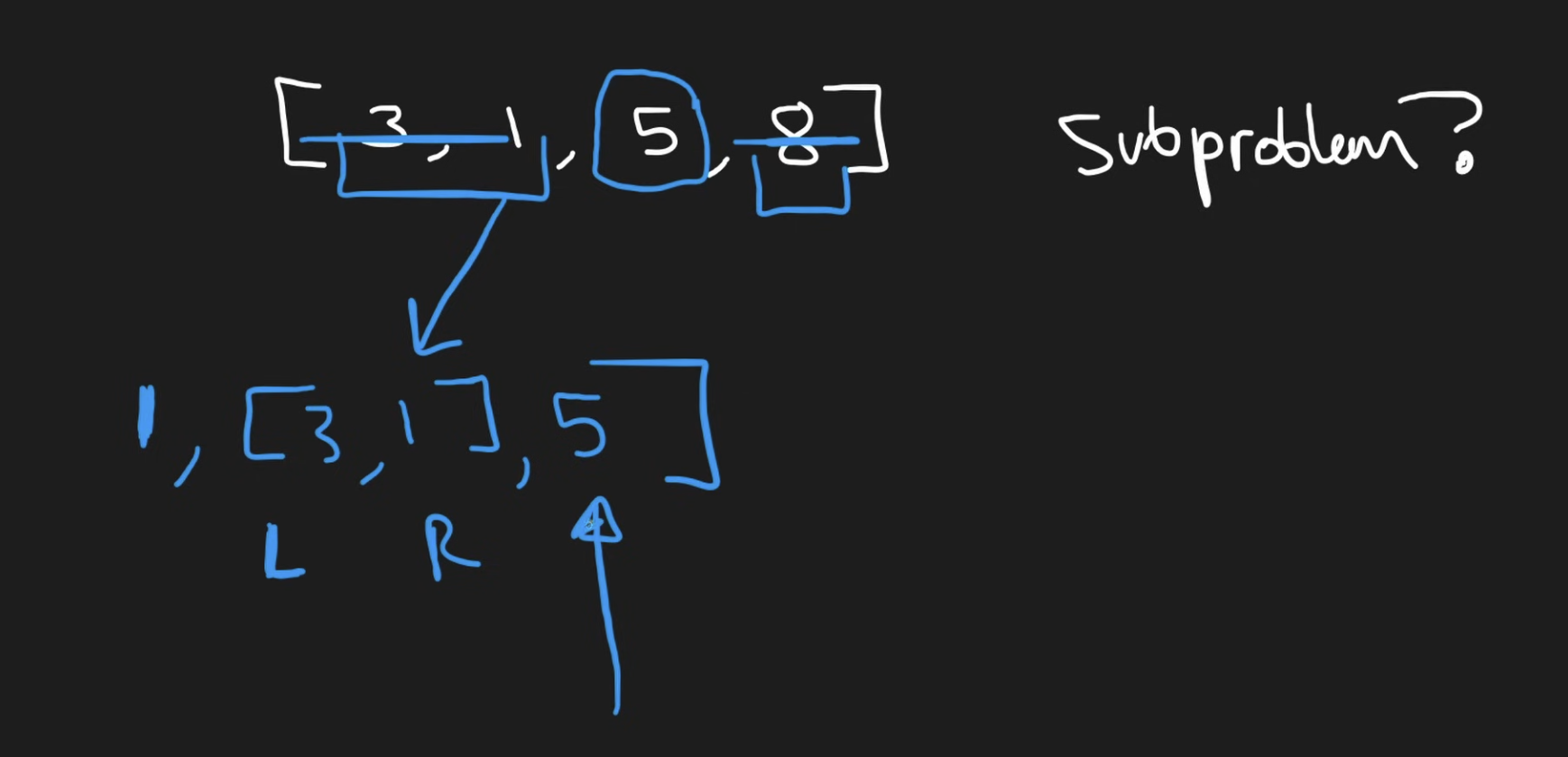
For general case, we consider the coins obtained with the ith coin and the ballon just outside the window (since by the time we finish processing, everything in the window except at iwould be empty.) We then add the coins from the 2 subarray. 
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
class Solution:
"""
brute force DFS
TLE
"""
def maxCoins(self, nums: List[int]) -> int:
nums = [1] + nums + [1]
def dfs(nums):
if len(nums) == 2:
return 0
max_coins = 0
for i in range(len(nums) - 1):
coins = nums[i - 1] * nums[i] * nums[i + 1]
coins += dfs(nums[:i] + nums[i+1:])
max_coins = max(max_coins, coins)
return max_coins
return dfs(nums)
class Solution:
"""
top down: memoization
TLE
"""
def maxCoins(self, nums: List[int]) -> int:
nums = [1] + nums + [1]
nums = tuple(nums)
cache = {}
def dfs(nums):
if len(nums) == 2:
return 0
if nums in cache:
return cache[nums]
max_coins = 0
for i in range(len(nums) - 1):
coins = nums[i - 1] * nums[i] * nums[i + 1]
coins += dfs(nums[:i] + nums[i+1:])
max_coins = max(max_coins, coins)
cache[nums] = max_coins
return cache[nums]
return dfs(nums)
class Solution:
"""
top down: memoization
noticed that here we pop the ith ballon last, so the boundary is different from above
the above solution is we pop the ballon first then we look at the sub problem
"""
def maxCoins(self, nums: List[int]) -> int:
nums = [1] + nums + [1]
cache = {}
# l and r are pointers of the original nums,
# i.e. not including the 1s at the side
def dfs(l, r):
if l > r:
return 0
if (l, r) in cache:
return cache[(l, r)]
max_coins = 0
for i in range(l , r + 1):
coins = nums[l - 1] * nums[i] * nums[r + 1]
coins += dfs(l, i - 1) + dfs(i + 1, r)
max_coins = max(max_coins, coins)
cache[(l, r)] = max_coins
return cache[(l, r)]
return dfs(1, len(nums) - 2)
class NeetSolution:
"""
bottom up solution
"""
def maxCoins(self, nums):
n = len(nums)
new_nums = [1] + nums + [1]
dp = [[0] * (n + 2) for _ in range(n + 2)]
for l in range(n, 0, -1):
for r in range(l, n + 1):
for i in range(l, r + 1):
coins = new_nums[l - 1] * new_nums[i] * new_nums[r + 1]
coins += dp[l][i - 1] + dp[i + 1][r]
dp[l][r] = max(dp[l][r], coins)
return dp[1][n]
Complexity
time: $O(n^3)$
space: $O(n^2)$