LC 329 - Longest Increasing Path in a Matrix

Question

Given an m x n integers matrix, return the length of the longest increasing path in matrix.

From each cell, you can either move in four directions: left, right, up, or down. You may not move diagonally or move outside the boundary (i.e., wrap-around is not allowed).

Example 1:

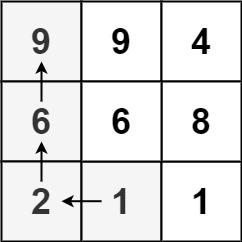
Input: matrix = [[9,9,4],[6,6,8],[2,1,1]]
Output: 4

Explanation: The longest increasing path is [1, 2, 6, 9].

Example 2:

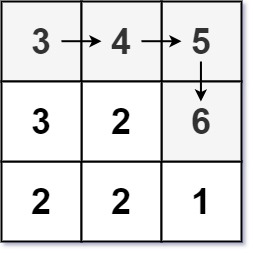
Input: matrix = [[3,4,5],[3,2,6],[2,2,1]]
Output: 4

Explanation: The longest increasing path is [3, 4, 5, 6]. Moving diagonally is not allowed.

Example 3:

Input: matrix = [[1]]
Output: 1

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• 0 <= matrix[i][j] <= 231 - 1

Links

Question here and solution here

Solution

concept

The top down solution is simple, just DFS with caching. There is no bottom up solution from NeetCode.

code

class Solution:
	"""
	brute force DFS
	TLE
	"""
    def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
        ROWS, COLS = len(matrix), len(matrix[0])
        directions = [(0,1), (1,0), (0,-1), (-1,0)]
		# no need visited set since we are looking for increasing, visited cell will be smaller than currently searching cell so it gets rejected
        def dfs(r, c, prev_val):
            if (r < 0 or r >= ROWS
                or c < 0 or c >= COLS 
                or matrix[r][c] <= prev_val):
                return 0
            
            ans = 1
            for dr, dc in directions:
                ans = max(ans, 1 + dfs(r + dr, c + dc, matrix[r][c]))
            
            return ans

        LIP = 0
        for r in range(ROWS):
            for c in range(COLS):
                LIP = max(LIP, dfs(r,c,-1))
        
        return LIP
        
class Solution:
	"""
	top down: memoization
	"""
    def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
        ROWS, COLS = len(matrix), len(matrix[0])
        directions = [(0,1), (1,0), (0,-1), (-1,0)]
        cache = {} # (r,c) -> LIP

        def dfs(r, c, prev_val):
            if (r < 0 or r >= ROWS
                or c < 0 or c >= COLS 
                or matrix[r][c] <= prev_val):
                return 0
            
            if (r,c) in cache:
                return cache[(r,c)]
            
            ans = 1
            for dr, dc in directions:
                ans = max(ans, 1 + dfs(r + dr, c + dc, matrix[r][c]))
            cache[(r,c)] = ans
            return cache[(r,c)]

        LIP = 0
        for r in range(ROWS):
            for c in range(COLS):
                LIP = max(LIP, dfs(r,c,-1))
        
        return LIP

Complexity

time: $O(mn)$
space: $O(mn)$