LC 48 - Rotate Image

Question

You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).

You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.

Example 1:

Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [[7,4,1],[8,5,2],[9,6,3]]

Example 2:

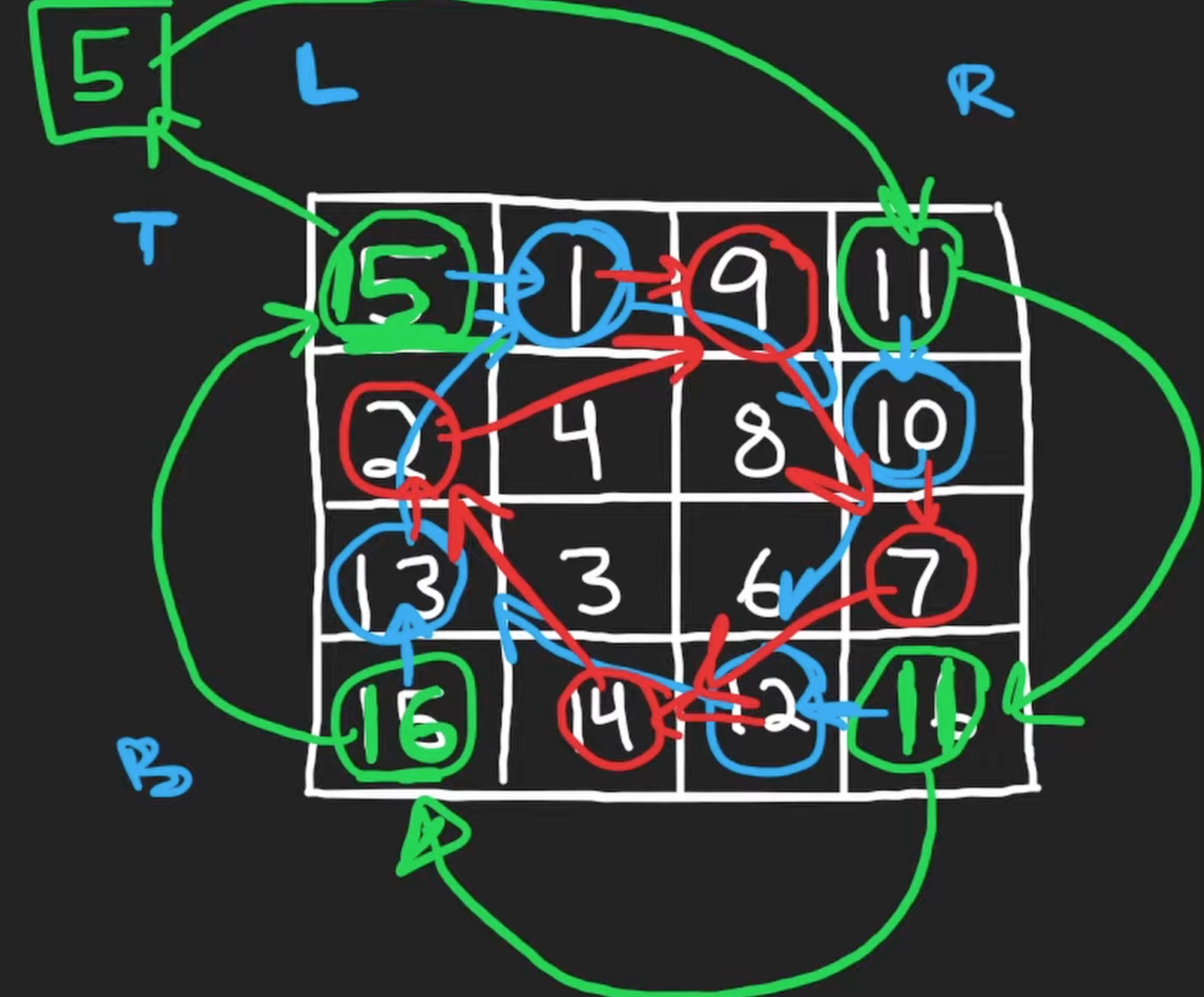
Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

Constraints:

• n == matrix.length == matrix[i].length
• 1 <= n <= 20
• -1000 <= matrix[i][j] <= 1000

Links

Question here and solution here

Solution

concept

There are two ways to accomplish this.

1. Rotate the matrix layer by layer: handle the outermost layers and then close in.
   1. we will maintain 4 pointers: l, r, top, bottom to mark the layer we are current handling
   2. we will do the rotation in reverse, so we only need to save one tmp variable (top_left cell in our case)
   3. we will use another variable i to keep track the cell movement as we are rotating the current layers
2. The mathematical equivalent is to reverse the matrix vertically and then do a transpose
   1. Since the given matrix is a square matrix, we only need to iterate over the upper triangular part, meaning the right upper portion of the main diagonal. In this way, we can transpose a matrix.

code

class Solution:
	"""
	brute force
	use an additional matrix to rotate first
	"""
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        n = len(matrix)
        rotated = [[0] * n for _ in range(n)]

        for i in range(n):
            for j in range(n):
                rotated[j][n - 1 - i] = matrix[i][j]

        for i in range(n):
            for j in range(n):
                matrix[i][j] = rotated[i][j]
                
class Solution:
	"""
	rotate the outer line of matrix, then close in
	"""
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        l, r = 0, len(matrix[0]) - 1

        while l < r:
            for i in range(r - l):
                top, bottom = l, r

                # save the top left
                top_left = matrix[top][l + i]
                # move bottom left to top left
                matrix[top][l + i] = matrix[bottom - i][l]
                # move bottom right to bottom left
                matrix[bottom - i][l] = matrix[bottom][r - i]
                # move top right to bottom right
                matrix[bottom][r - i] = matrix[top + i][r]
                # move saved top left to top right
                matrix[top + i][r] = top_left
            l += 1
            r -= 1
            
class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.

        transpose the matrix and then reverse each row
        
        only handle top right corner for transpose
        """
        #transpose 
        for row in range(len(matrix)):
            for col in range(row,len(matrix)):
                temp = matrix[row][col]
                matrix[row][col] = matrix[col][row]
                matrix[col][row] = temp

        #reverse
        for row in matrix:
            row.reverse()
    
class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        # Reverse the matrix vertically
        matrix.reverse()

        # Transpose the matrix
        for i in range(len(matrix)):
            for j in range(i + 1, len(matrix)):
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]

Complexity

time: $O(n)$
space: $O(n)$