LC 494 - Target Sum

Question

You are given an integer array nums and an integer target.

You want to build an expression out of nums by adding one of the symbols '+' and '-' before each integer in nums and then concatenate all the integers.

• For example, if nums = [2, 1], you can add a '+' before 2 and a '-' before 1 and concatenate them to build the expression "+2-1".

Return the number of different expressions that you can build, which evaluates to target.

Example 1:

Input: nums = [1,1,1,1,1], target = 3
Output: 5

Explanation: There are 5 ways to assign symbols to make the sum of nums be target 3. -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3

Example 2:

Input: nums = [1], target = 1
Output: 1

Constraints:

• 1 <= nums.length <= 20
• 0 <= nums[i] <= 1000
• 0 <= sum(nums[i]) <= 1000
• -1000 <= target <= 1000

Links

Question here and solution here

Solution

concept

The bottom up solution requires a 2D grid where the y-axis is the the index i same as the DFS solution. and the x-axis is the cur_sum that is possible to sum with the current number at ith index It is defined that the first row at 0 will be 0, this means one way to sum to 0 with the first 0 elements, the number in the grid itself represent the number of ways it can be used to sum. We do not need to populate the whole grid (hence in this question the dp is a defaultdict) We are only interested in the purple box number which is the answer (i.e. after we go through all 5 numbers, the target sum is 3, and what is the total number of ways ?)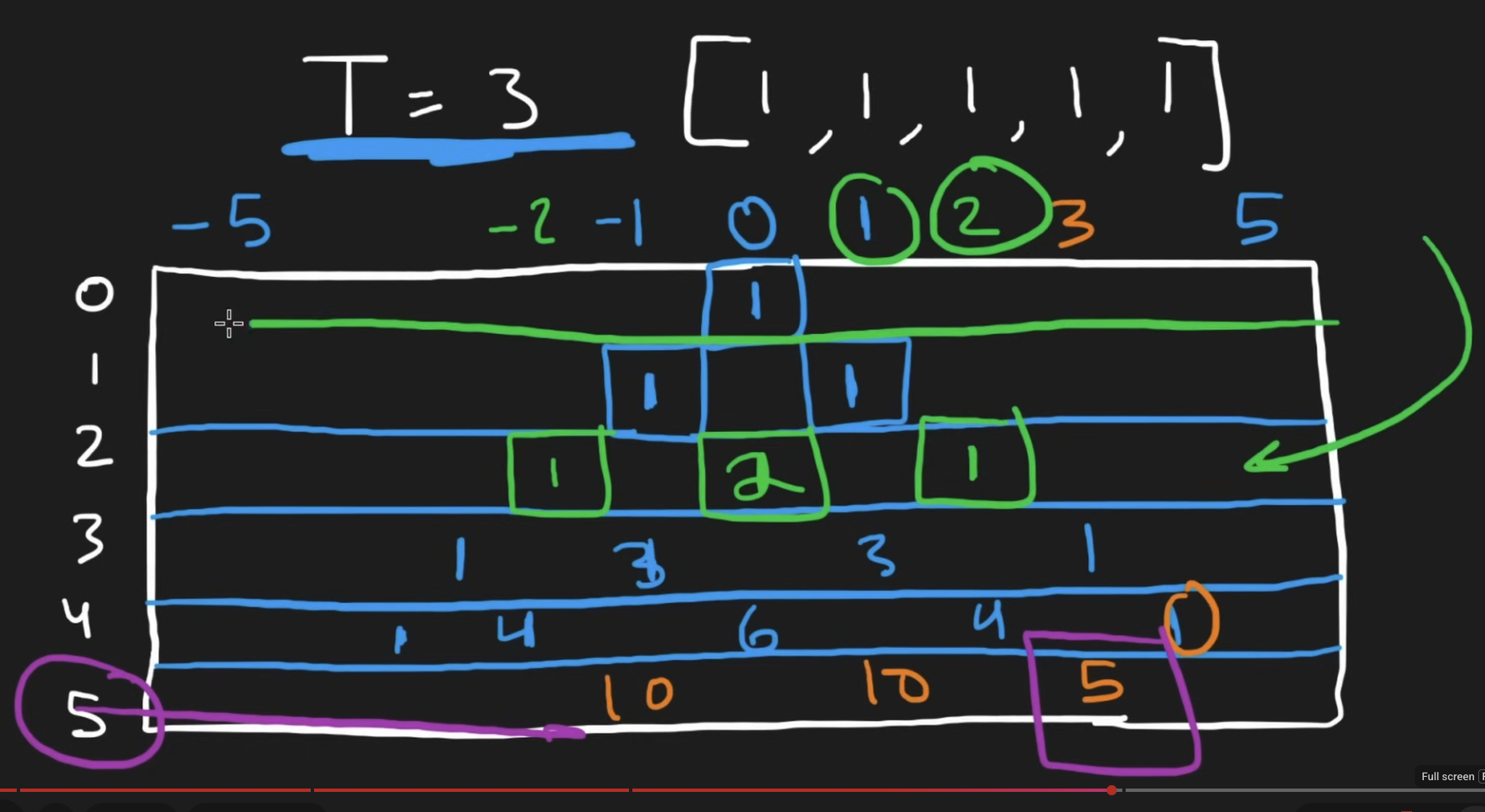

For the space optimized solution, notice that we only need the previous row to compute the next row.

code

class Solution:
	"""
	brute force dfs
	TLE
	"""
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        
        def dfs(i, cur_sum):
            if i >= len(nums):
                if cur_sum == target:
                    return 1
                else:
                    return 0
            
            plus_option = dfs(i + 1, cur_sum + nums[i])
            minus_option = dfs(i + 1, cur_sum - nums[i])

            return plus_option + minus_option

        return dfs(0, 0)

class Solution:
	"""
	top down: memoization
	"""
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        cache = {}
        def dfs(i, cur_sum):
            if (i, cur_sum) in cache:
                return cache[(i, cur_sum)]
            if i >= len(nums):
                if cur_sum == target:
                    return 1
                else:
                    return 0
            
            plus_option = dfs(i + 1, cur_sum + nums[i])
            minus_option = dfs(i + 1, cur_sum - nums[i])
            cache[(i, cur_sum)] = plus_option + minus_option
            return cache[(i, cur_sum)]

        return dfs(0, 0)
        
class Solution:
	"""
	bottom up solution
	"""
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        dp = [defaultdict(int) for i in range(len(nums) + 1)]
        dp[0][0] = 1 # one way to sum to 0 with first 0 element

        for i in range(len(nums)):
            for cur_sum, count in dp[i].items():
                dp[i + 1][cur_sum + nums[i]] += count
                dp[i + 1][cur_sum - nums[i]] += count
        
        return dp[len(nums)][target]
        
class Solution:
	"""
	bottom up solution
	space optimized
	"""
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        dp = defaultdict(int)
        dp[0] = 1 # one way to sum to 0

        for i in range(len(nums)):
            next_dp = defaultdict(int)
            for cur_sum, count in dp.items():
                next_dp[cur_sum + nums[i]] += count
                next_dp[cur_sum - nums[i]] += count
            dp = next_dp
        
        return dp[target]

Complexity

time: $O(nm)$
space: $O(nm)$ or $O(m)$
where n is the length of the array nums and m is the sum of all the elements in the array