LC 51 - N-Queens

Question

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens’ placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.

Example 1:

Input: n = 4
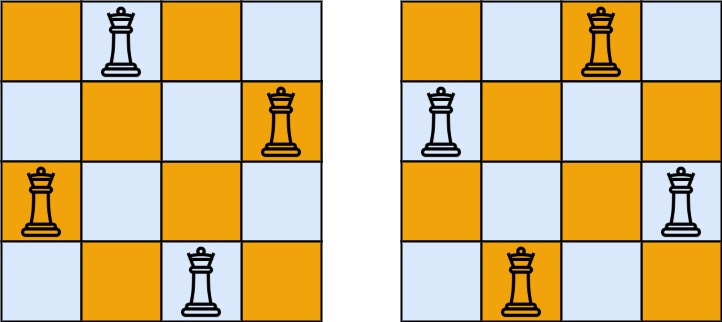
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] **Explanation:** There exist two distinct solutions to the 4-queens puzzle as shown above

Example 2:

Input: n = 1
Output: [["Q"]]

Constraints:

• 1 <= n <= 9

Links

Question here and solution here

Solution

concept

This question uses backtracking to go through each row and maintaining 3 sets

1. check all the columns such that we do not place a queen in existing column
2. positive diagonal (gradient increasing), notice that r + c is constant for the same diagonal, we can use it to track
3. negative diagonal wherer - c is constant, which we can use it to track

We DFS through each row, and within each row, we iterate through each column and keep track the sets

code

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        col_set = set()
        pos_diag_set = set()
        neg_diag_set = set()
        board = [["."] * n for _ in range(n)]
        ans = []

        def backtrack(r):
            if r == n:
                tmp = ["".join(row) for row in board]
                ans.append(tmp)
                return

            for c in range(n):
                if c in col_set or r + c in pos_diag_set or r - c in neg_diag_set:
                    continue
                
                col_set.add(c)
                pos_diag_set.add(r + c)
                neg_diag_set.add(r - c)
                board[r][c] = "Q"

                backtrack(r + 1)

                col_set.remove(c)
                pos_diag_set.remove(r + c)
                neg_diag_set.remove(r - c)
                board[r][c] = "."

        backtrack(0)
        return ans

Complexity

time: $O(n!)$
space: $O(n^2)$