LC 54 - Spiral Matrix

Question

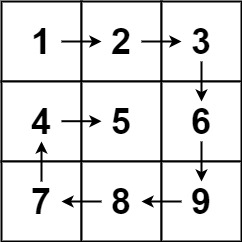
Given an m x n matrix, return all elements of the matrix in spiral order.

Example 1:

Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,3,6,9,8,7,4,5]

Example 2:

Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 10
• -100 <= matrix[i][j] <= 100

Links

Question here and solution here

Solution

concept

We will follow the path of the spiral matrix to append each cell. The only trick is to use 4 pointers to mark the current layers we are working on. The tricky part of the question are all the off-by-1 error when we are keep tracking of all the pointers.

code

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        """
        the right and bottom boundary is set out of bound by 1 for easier calculation 
        """
        result = []
        top, bottom = 0, len(matrix) # out of bound by 1
        left, right = 0, len(matrix[0]) # out of bound by 1

        while left < right and top < bottom:
            # top row, right -> left
            for i in range(left, right):
                result.append(matrix[top][i])
            top += 1

            # right col, up - > bottom
            for i in range(top, bottom):
                result.append(matrix[i][right - 1])
            right -= 1
            
            # need to check in between else error
            # for edge case: col and row vector
            if not (left < right and top < bottom):
                break

            # bottom row: right -> left
            # note the off-by-1
            for i in range(right - 1, left - 1, -1):
                result.append(matrix[bottom - 1][i])
            bottom -= 1

            # left col: bottom -> up
            for i in range(bottom - 1, top - 1, -1):
                result.append(matrix[i][left])
            left += 1

        return result

Complexity

time: $O(mn)$
space: $O(1)$