LC 543 - Diameter of Binary Tree
Question
Given the root of a binary tree, return the length of the diameter of the tree.
The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.
The length of a path between two nodes is represented by the number of edges between them.
Example 1:
1
2
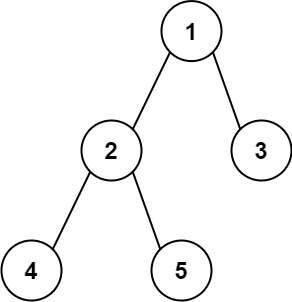
Input: root = [1,2,3,4,5]
Output: 3
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].
Example 2:
1
2
Input: root = [1,2]
Output: 1
Constraints:
- The number of nodes in the tree is in the range
[1, 104]. -100 <= Node.val <= 100
Links
Question here and solution here
Solution
concept
This question is a bit similar to [[104. Maximum Depth of Binary Tree]] in the sense we would like to keep track the depth or height of the tree. The easy way is to use DFS to traverse the tree. The key thing here is to keep track the diameter in a global variable but in the DFS function we return the height of the tree. The reason is we can get the diameter by adding the left and right height of the current node and height is sort of invariant in the calculation here. If we return maximum diameter, this maximum length path might not even pass the current root, but by keeping the height from both side, we can keep track the diameter.
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
self.ans = 0
def dfs(curr):
if not curr:
return 0 # height of the current tree
h_left = dfs(curr.left)
h_right = dfs(curr.right)
self.ans = max(self.ans, h_left + h_right)
return 1 + max(h_left, h_right)
dfs(root)
return self.ans
Complexity
Time complexity: $O(n)$ Space complexity: $O(h)$
- Best Case (balanced tree): $O(\log(n))$
- Worst Case (degenerate tree): $O(n)$