LC 572 - Subtree of Another Tree

Question

Given the roots of two binary trees root and subRoot, return true if there is a subtree of root with the same structure and node values of subRoot and false otherwise.

A subtree of a binary tree tree is a tree that consists of a node in tree and all of this node’s descendants. The tree tree could also be considered as a subtree of itself.

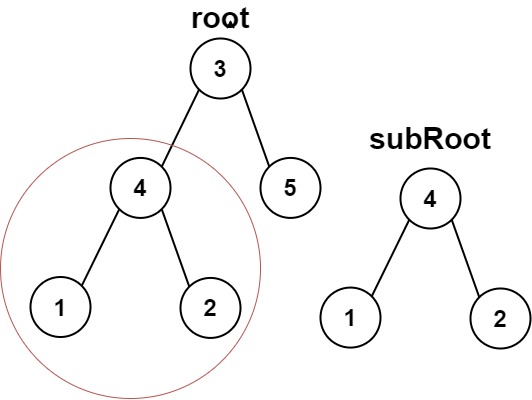
Example 1:

Input: root = [3,4,5,1,2], subRoot = [4,1,2]
Output: true

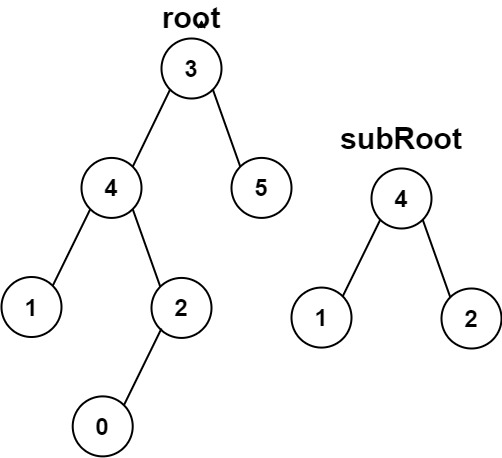
Example 2:

Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
Output: false

Constraints:

• The number of nodes in the root tree is in the range [1, 2000].
• The number of nodes in the subRoot tree is in the range [1, 1000].
• -104 <= root.val <= 104
• -104 <= subRoot.val <= 104

Links

Question here and solution here

Solution

concept

We can borrow the idea from [[100. Same Tree]] and iterate through all the nodes and check if any sub tree starting from that node (i.e. that node as the root) match the subRoot.

code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
        self.ans = False
        def same_tree(root_1, root_2):
            if not root_1 and not root_2:
                return True
            elif not root_1 or not root_2:
                return False
            elif root_1.val != root_2.val:
                return False

            left_check = same_tree(root_1.left, root_2.left)
            right_check = same_tree(root_1.right, root_2.right)

            return left_check and right_check

        def dfs(root):
            if not root:
                return
            if root.val == subRoot.val:
                same = same_tree(root, subRoot)
                if same:
                    self.ans = same
            dfs(root.left)
            dfs(root.right)

        dfs(root)
        return self.ans
        
class Solution:
    """
    For each node in the main tree, check if the subtree is same as the subroot.
    """
    def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
        # If the main tree is empty, or it reached the end of the main tree, return False
        if not root:
            return False
        # check if the current node (and its children) is the same as the subroot
        if self.isSameTree(root, subRoot):
            return True
        # check if the subtree is in the left or right of the main tree
        main_left_check = self.isSubtree(root.left, subRoot)
        main_right_check = self.isSubtree(root.right, subRoot)
        # either left or right branch return True then it will be true
        return (main_left_check or main_right_check)

    def isSameTree(self, root, subroot):
        """
        same as Qn 100: Same Tree
        """
        if not root and not subroot:
        # this covers the edge case where root is not None but subroot is None -> yes it is subtree
        # think of it the leaf node will lead to None child node which is the same as the (Null) subroot
        # this also covers the edge case where both root and subroot are None -> yes it is subtree
            return True
        elif not root or not subroot:
            return False
        elif root.val != subroot.val:
            return False

        left_check = self.isSameTree(root.left, subroot.left)
        right_check = self.isSameTree(root.right, subroot.right)

        return (left_check and right_check)
        
class NeetSolution:
    """
    time complexity: O(n * m) where n is the number of nodes in the main tree and m is the number of nodes in the subtree
    """
    
    def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
        if not subRoot:  # edge case that a null tree is a subTree of tree
            return True
        # order matters, here is really "if not root and subRoot", but subRoot is checked in the first if statement
        # this if statement is necessary for isSubtree to backtrack when it reaches the end of main tree
        # it also covers the edge case where root is None but subRoot is not None -> no, not a subtree
        # although the this case is also covered in the (return) exit condition of the sameTree function
        if not root:
            return False

        if self.sameTree(root, subRoot):
            return True
        return self.isSubtree(root.left, subRoot) or self.isSubtree(root.right, subRoot)

    def sameTree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
        if not root and not subRoot:
            return True
        if root and subRoot and root.val == subRoot.val:
            return self.sameTree(root.left, subRoot.left) and self.sameTree(root.right, subRoot.right)
        # this means that one of the root/subRoot is None and the other is not, hence not the same tree
        return False

Complexity

time: $O(m*n)$
space: $O(m+n)$