LC 684 - Redundant Connection

Question

In this problem, a tree is an undirected graph that is connected and has no cycles.

You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.

Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.

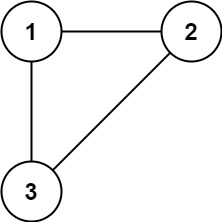
Example 1:

Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]

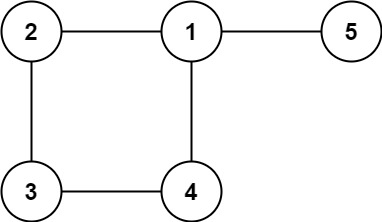
Example 2:

Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
Output: [1,4]

Constraints:

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ai < bi <= edges.length
• ai != bi
• There are no repeated edges.
• The given graph is connected.

Links

Question here and solution here

Solution

concept

Use DFS solution on each node in the given edge and search for cycles.

code

class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        n = len(edges)
        adj_list = {i : [] for i in range(1,n + 1)}
 
        def dfs(node, parent):
            if node in visited:
                return True
            
            visited.add(node)
            for nei in adj_list[node]:
                if nei == parent:
                    continue
                if dfs(nei, node):
                    return True # found the cycle
            return False
        
        for n1, n2 in edges:
            adj_list[n1].append(n2)
            adj_list[n2].append(n1)
            visited = set()

            if dfs(n1, -1):
                return [n1, n2]
        return []

Complexity

time: $O(E(V+E))$
space: $O(V+E)$