LC 70 - Climbing Stairs

Question

You are climbing a staircase. It takes n steps to reach the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Example 1:

Input: n = 2
Output: 2

Explanation: There are two ways to climb to the top.

1. 1 step + 1 step
2. 2 steps

Example 2:

Input: n = 3
Output: 3

Explanation: There are three ways to climb to the top.

1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

Constraints:

• 1 <= n <= 45

Links

Question here and solution here

Solution

concept

From the example of n=5, we can see that this is a decision tree where at each step we can choose to go 1 step or 2 step. But We can see that there are repeated work in the tree (i.e. the two purple sub tree are the same).

Furthermore, there are more subtree that are duplicated as shown below: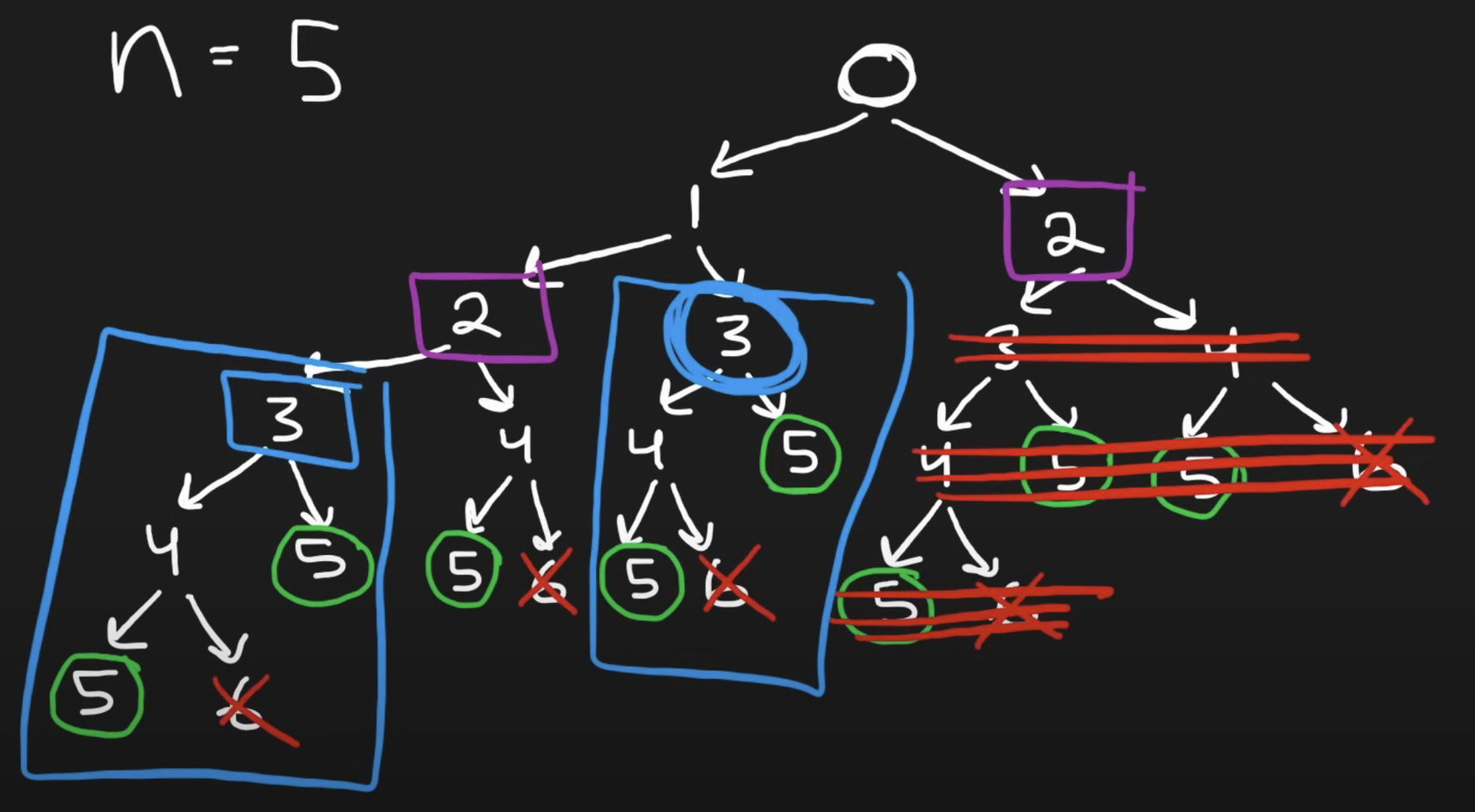

Essentially we only need to compute the solution in $O(n)$:

The bottom-up DP solution: the base case is the last two steps where step_5 is the base case itself with 1 way to reach itself and step_4 has 1 way to reach step_5 by using 1 step. From here on, we note that from step_3 we can reach either step_4 and step_5 and we will not re-calculate how many ways we can reach the goal from step_4 and step_5: the ways from step_3 is the sum of the ways from step_4 and step_5 since these are the 2 choices.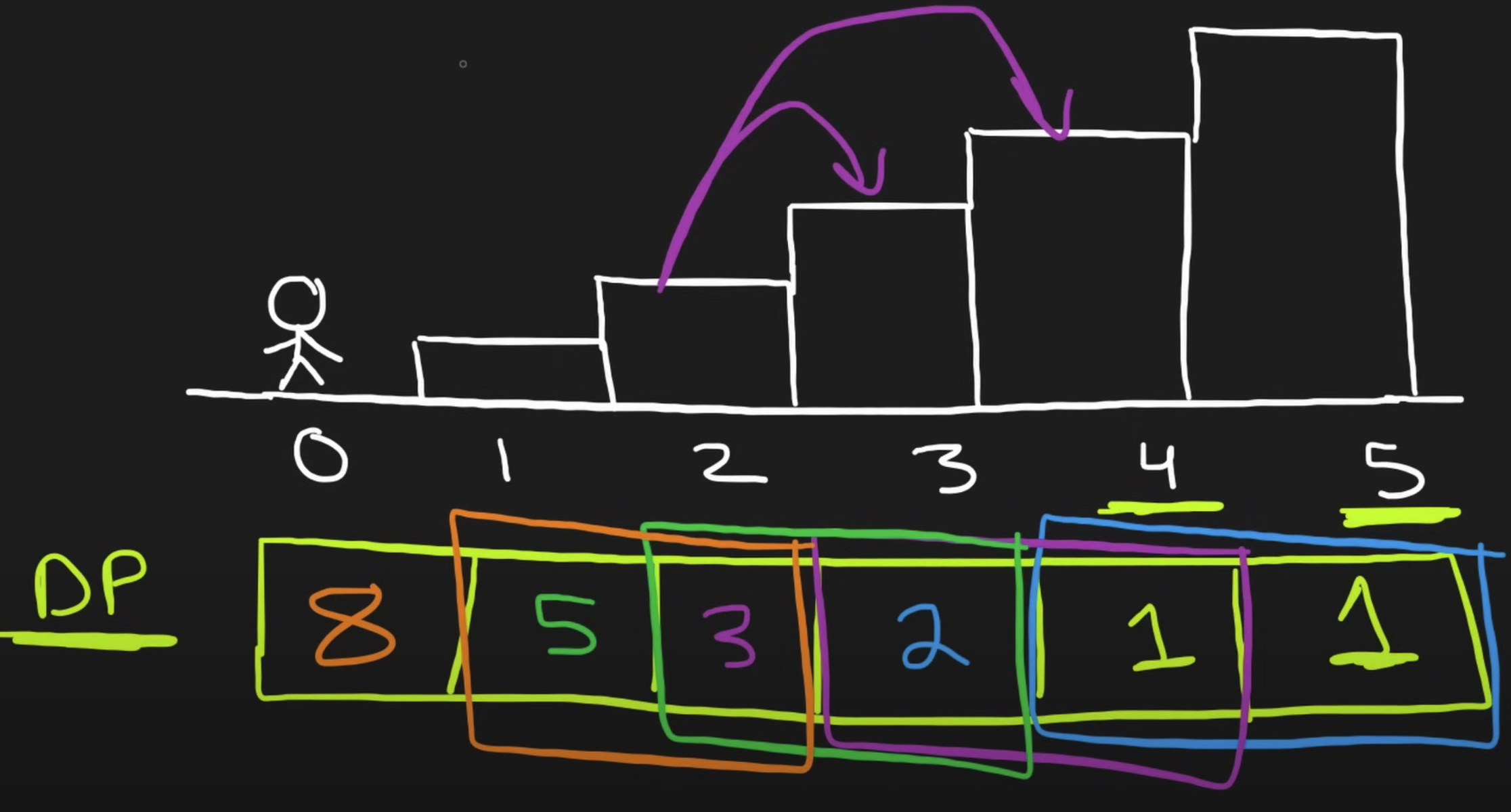

code

class Solution:
	"""
	Brute Force DFS
	"""
    def climbStairs(self, n: int) -> int:
            
        def dfs(i):
            if i == n:
                return 1
            if i > n:
                return 0
                
            return dfs(i + 1) + dfs(i + 2)
        
        return dfs(0)

class Solution:
	"""
	Top down DP (memoization)
	"""
    def climbStairs(self, n: int) -> int:
        cache = [-1] * n
        def dfs(i):
            if i >= n:
                return i == n
            if cache[i] != -1:
                return cache[i]
            cache[i] = dfs(i + 1) + dfs(i + 2)
            return cache[i]

        return dfs(0)

class Solution:
	"""
	bottom up dp (space optimised)
	solving from right -> left
	"""
    def climbStairs(self, n: int) -> int:
        one_step, two_step = 1, 1
        for _ in range(n - 1):
            tmp = one_step
            one_step = one_step + two_step
            two_step = tmp

        return one_step
        
class Solution:
	"""
	bottom up
	solving from right -> left
	"""
    def climbStairs(self, n: int) -> int:
        if n <= 2:
            return n
        dp = [1] * (n + 1)
        # start from the 3rd last index, base case is [1,1] for the last 2 index
        # n - 2 is actually (n+1)-3
        for i in range(n - 2, -1, -1):
            dp[i] = dp[i+1] + dp[i+2]

        return dp[0]

Complexity

time: $O(n)$
space: $O(n)$