LC 72 - Edit Distance

Question

Given two strings word1 and word2, return the minimum number of operations required to convert word1 to word2.

You have the following three operations permitted on a word:

• Insert a character
• Delete a character
• Replace a character

Example 1:

Input: word1 = "horse", word2 = "ros"
Output: 3

Explanation: horse -> rorse (replace ‘h’ with ‘r’) rorse -> rose (remove ‘r’) rose -> ros (remove ‘e’)

Example 2:

Input: word1 = "intention", word2 = "execution"
Output: 5

Explanation: intention -> inention (remove ‘t’) inention -> enention (replace ‘i’ with ‘e’) enention -> exention (replace ‘n’ with ‘x’) exention -> exection (replace ‘n’ with ‘c’) exection -> execution (insert ‘u’)

Constraints:

• 0 <= word1.length, word2.length <= 500
• word1 and word2 consist of lowercase English letters.

Links

Question here and solution here

Solution

concept

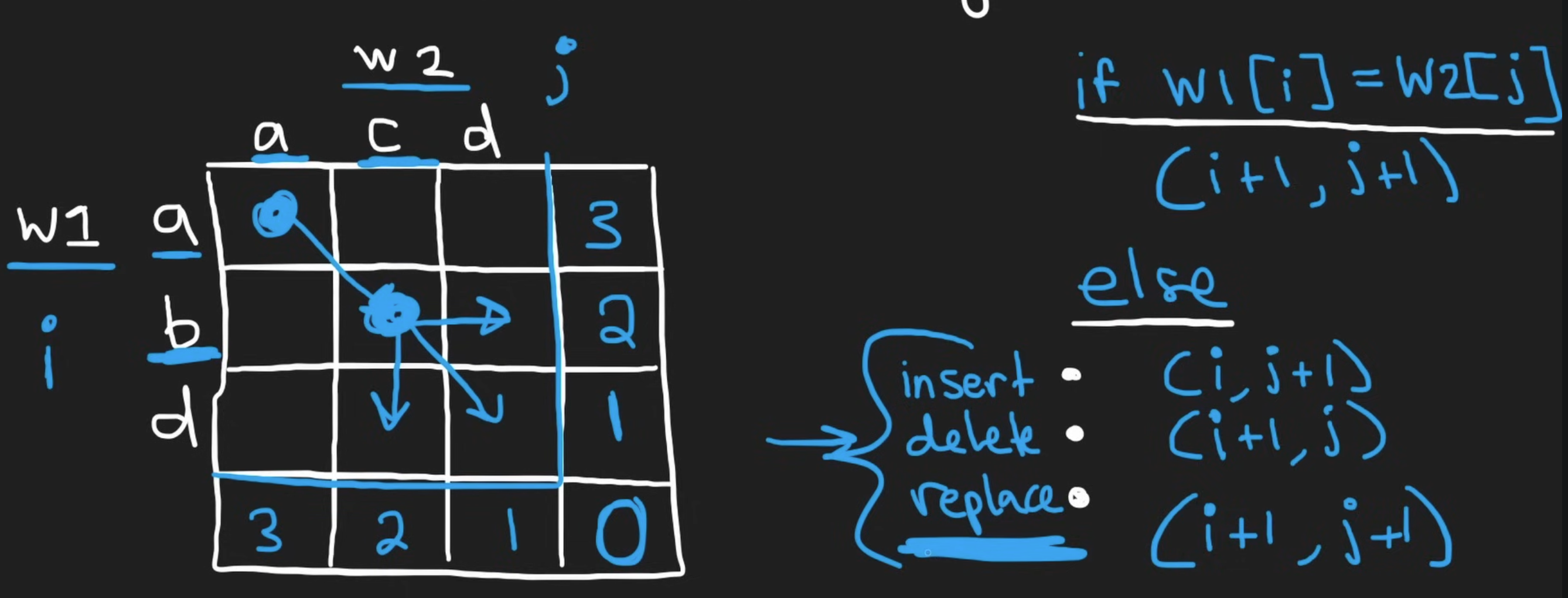
If we have two words word1 and word2, and i and j are the index respectively, we will have a few scenario if we want to make word1 -> word2:

1. if word1[i] == word2[j], then there is no operation needed.
   1. we need to shift both pointers since they are matched: (i,j) -> (i+1,j+1)
2. if word1[i] != word2[j], then there will be one operation needed to operate on word1, we will go down all three path, but each with different pointer movement:
   1. insert: our i pointer stays the same since we just insert a char at index i, but since after inserting word2 at j is satisfied, we have to move the j pointer:
      1. (i, j) -> (i, j+1)
   2. delete: this is the same as skipping the current char in word1, but since there is no match in word2 yet, so the j pointer remains the same:
      1. (i, j) -> (i+1, j)
   3. replace: this means that we are able to match after replacing, so both pointers advanced. The difference between this and the already-matched in the first case is that this one needs one operation and the already-matched does not need an operation
      1. (i, j) -> (i+1, j+1)

The base case will be either word run out:

1. if word1 run out first, this means that i has reached the end, then the number of operations needed is inserting the remaining of the word2 into word1, this means the operations needed is len(word2) - j
2. if word2 run out first, this means that j has reached the end, then the number of operations needed is deleting the remaining of the word1 such that it is equal to word2, this means the operations needed is len(word1) - i

For the bottom up solution, the concept is very similar:

1. at each cell, we record the minimum number of operations needed for the sub problems for word1[i:] and word2[j:]
2. we have our base cases at the right and bottom and it is basically the cases where either string runs out. This is the same base cases as the above
3. if word1[i] == word2[j] then we just take the diagonal bottom right
4. else we will take look at the 3 squares and find the minimum of these and add one operation on top of it.

code

class Solution:
	"""
	brute force DFS
	TLE
	"""
    def minDistance(self, word1: str, word2: str) -> int:
        
        def dfs(i,j):
            if i == len(word1):
                return len(word2) - j
            if j == len(word2):
                return len(word1) - i
            
            # already matched
            if word1[i] == word2[j]:
                return dfs(i + 1, j + 1) # no operation needed
            
            # choose the min among the three operations
            ops = min(dfs(i + 1, j), dfs(i, j + 1), dfs(i + 1, j + 1))

            return 1 + ops # one operation needed
        
        return dfs(0,0)

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
	    """
	    top down: memoization
	    """
        cache = {}
        def dfs(i,j):
            if i == len(word1):
                return len(word2) - j
            if j == len(word2):
                return len(word1) - i
            if (i,j) in cache:
                return cache[(i, j)]
            
            if word1[i] == word2[j]:
                cache[(i,j)] = dfs(i + 1, j + 1)
                return cache[(i,j)] 
            
            ops = min(dfs(i + 1, j), dfs(i, j + 1), dfs(i + 1, j + 1))
            cache[(i,j)] = 1 + ops
            return cache[(i,j)]
        
        return dfs(0,0)

class Solution:
	"""
	bottom up solution
	"""
    def minDistance(self, word1: str, word2: str) -> int:
        dp = [[float("inf")] * (len(word2) + 1) for _ in range(len(word1) + 1)]

        for i in range(len(word1) + 1):
            dp[i][len(word2)] = len(word1) - i
        for j in range(len(word2) + 1):
            dp[len(word1)][j] = len(word2) - j

        for i in range(len(word1)-1, -1, -1):
            for j in range(len(word2)-1, -1, -1):
                if word1[i] == word2[j]:
                    dp[i][j] = dp[i + 1][j + 1]
                else:
                    dp[i][j] = 1 + min(dp[i + 1][j + 1], dp[i][j + 1], dp[i + 1][j])
        
        return dp[0][0]

class NeetSolution:
	"""
	bottom up solution
	space optimized
	"""
    def minDistance(self, word1: str, word2: str) -> int:
        m, n = len(word1), len(word2)
        if m < n:
            m, n = n, m
            word1, word2 = word2, word1

        dp = [0] * (n + 1)
        nextDp = [0] * (n + 1)

        for j in range(n + 1):
            dp[j] = n - j

        for i in range(m - 1, -1, -1):
            nextDp[n] = m - i
            for j in range(n - 1, -1, -1):
                if word1[i] == word2[j]:
                    nextDp[j] = dp[j + 1]
                else:
                    nextDp[j] = 1 + min(dp[j], nextDp[j + 1], dp[j + 1])
            dp = nextDp[:]

        return dp[0]

Complexity

time: $O(mn)$
space: $O(mn)$ or $O(min(m,n))$