LC 74 - Search a 2D Matrix

Question

You are given an m x n integer matrix matrix with the following two properties:

• Each row is sorted in non-decreasing order.
• The first integer of each row is greater than the last integer of the previous row.

Given an integer target, return true if target is in matrix or false otherwise.

You must write a solution in O(log(m * n)) time complexity.

Example 1:

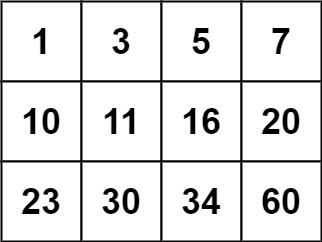
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

Example 2:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -104 <= matrix[i][j], target <= 104

Links

Question here and solution here

Solution

concept

The main concept here is to use binary search. The easiest way is to make it into a 1-D array and apply normal binary search.
The more fancy way is to implement 2-D binary search: binary search on row first to determine which row can start on the search, then search that row.

code

class Solution:
	"""
	convert into 1-D array and then do binary search
	"""
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        arr = []
        for lst in matrix:
            arr.extend(lst)

        l, r = 0, len(arr) - 1
        while l <= r:

            mid = (l+r)//2
            if arr[mid] == target:
                return True
            elif arr[mid] > target:
                r = mid - 1
            else:
                l = mid + 1
        return False
        
class Solution:
	"""
	2-D binary search
	"""
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        ROWS, COLS = len(matrix), len(matrix[0])

        up, down = 0, ROWS - 1
        while up <= down:
            row_mid = (up + down) // 2
            if matrix[row_mid][0] > target:
                down = row_mid - 1
            elif matrix[row_mid][-1] < target:
                up = row_mid + 1
            else:
                break

        left, right = 0, COLS - 1
        while left <= right:
            col_mid = (left + right) // 2
            if matrix[row_mid][col_mid] > target:
                right = col_mid - 1
            elif matrix[row_mid][col_mid] < target:
                left = col_mid + 1
            else:
                return True

        return False

Complexity

time: $O(\log (m*n))$ space: $O(\log (m * n))$