LC 778 - Swim in Rising Water

Question

You are given an n x n integer matrix grid where each value grid[i][j] represents the elevation at that point (i, j).

It starts raining, and water gradually rises over time. At time t, the water level is t, meaning any cell with elevation less than equal to t is submerged or reachable.

You can swim from a square to another 4-directionally adjacent square if and only if the elevation of both squares individually are at most t. You can swim infinite distances in zero time. Of course, you must stay within the boundaries of the grid during your swim.

Return the minimum time until you can reach the bottom right square (n - 1, n - 1) if you start at the top left square (0, 0).

Example 1:

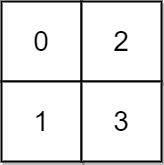
Input: grid = [[0,2],[1,3]]
Output: 3

Explanation: At time 0, you are in grid location (0, 0). You cannot go anywhere else because 4-directionally adjacent neighbors have a higher elevation than t = 0. You cannot reach point (1, 1) until time 3. When the depth of water is 3, we can swim anywhere inside the grid.

Example 2:

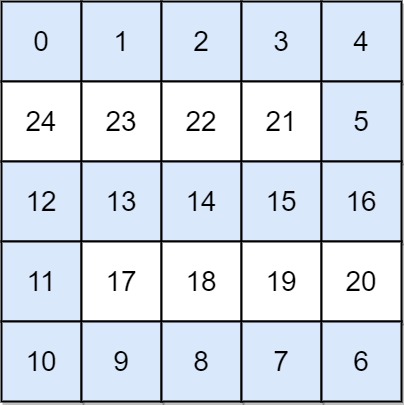
Input: grid = [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
Output: 16

Explanation: The final route is shown. We need to wait until time 16 so that (0, 0) and (4, 4) are connected.

Constraints:

• n == grid.length
• n == grid[i].length
• 1 <= n <= 50
• 0 <= grid[i][j] < n2
• Each value grid[i][j] is unique.

Links

Question here and solution here

Solution

concept

This problem actually reduced to finding the path from start to end with the minimum height (in the path), since we can swim with infinite amount of speed.

The main concept is to use a variations of Dijkstra’s algorithm similar to [[743. Network Delay Time]]. The difference here is how we store in the min heap. Here we store the maximum height so far in each steps.

Note that here we add the square into the visited set the moment we add them into the min heap (which is different from [[743. Network Delay Time]]). Only adding the square after popping from the heap will probably also works but it gets TLE. Since every path start from the same square and we are minimising the height at each step, the moment we add in the heap it is the minimum height for that (r,c), i.e. the minimum height so far from starting point to that (r,c). If we put the adding to visited set after popping, there will be multiple adding into the heap and searching, which will cost TLE.

code

class Solution:
    def swimInWater(self, grid: List[List[int]]) -> int:
        N = len(grid)
        visited = set()
        visited.add((0,0))
        min_heap = [(grid[0][0], 0, 0)] # (max_height_so_far, r, c)
        directions = [(0,1), (1,0), (0,-1),(-1,0)]

        while min_heap:
            h, r, c = heapq.heappop(min_heap)
            # reached goal
            if r == N - 1 and c == N - 1:
                return h
            # probably works but TLE
            # visited.add((r, c))

            # explore 4 dir
            for dr, dc in directions:
                n_r, n_c = r + dr, c + dc
                if (n_r < 0 or n_c < 0 or
                    n_r >= N or n_c >= N or
                    (n_r, n_c) in visited):
                    continue
                
                visited.add((n_r, n_c))
                heapq.heappush(min_heap, (max(h, grid[n_r][n_c]),n_r, n_c))

Complexity

time: $O(n^2 \log n)$
space: $O(n^2)$