LC 84 - Largest Rectangle in Histogram

Question

Given an array of integers heights representing the histogram’s bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.

Example 1:

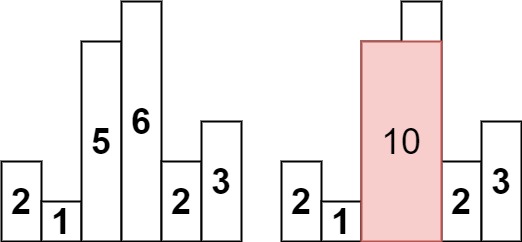
Input: heights = [2,1,5,6,2,3]
Output: 10

Explanation: The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.

Example 2:

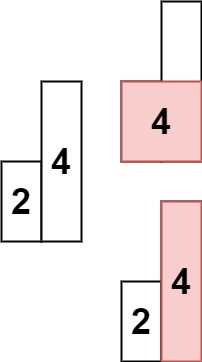
Input: heights = [2,4]
Output: 4

Constraints:

• 1 <= heights.length <= 105
• 0 <= heights[i] <= 104

Links

Question here and solution here

Solution

concept

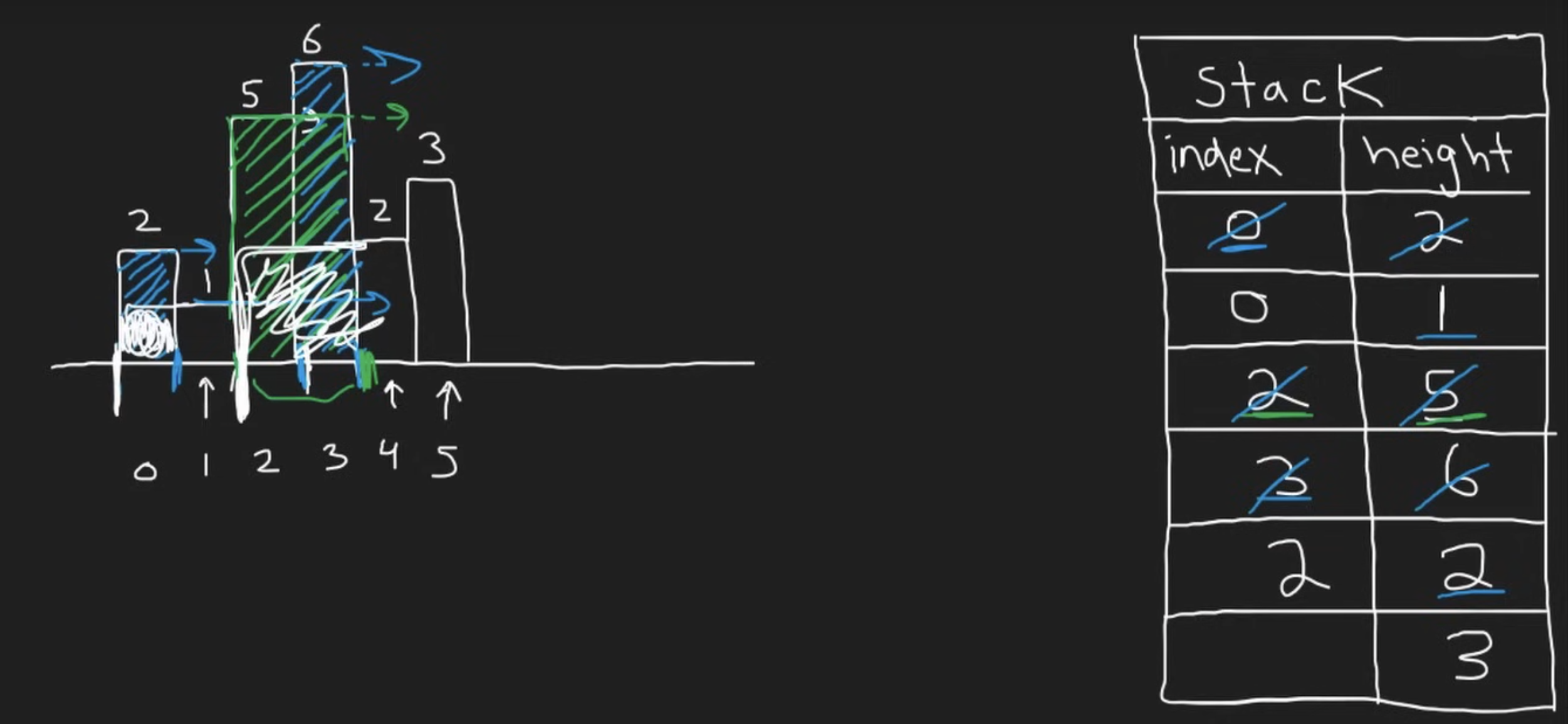
The main idea is to use a stack to keep track of both the index and the height of the current bar. Note that there is 2 things we should take care:

1. if the current bar’s height is higher (or equal) than the previous one (i.e. stack[-1]), this means the previous bar can still “penetrate through the current bar” and it should be kept
2. if the current bar’s height is lower than the previous one, this means the previous bar’s rectangle will be stopped by the current bar, so its rectangle area should be calculated and then pop from the stack. We only need to take care the area starting from the popped bar to the right, the left side of the popped bar will be lower than it by design, so the rectangle will NOT extend to the left.
3. whenever we pop a bar, we need to take note of its starting point, the newly added bar can be extended to the left since these bar is all higher (note the bar at index=4 can be extended all the way to index = 2), when we add the current bar into the stack, its index needs to be adjusted to account for the missing space by the popped bars.

At the end of the operations, there are still bars left and these bars can be extended all the way to the right, so we need to iterate through these bars to get the area.

code

class NeetSolution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        """
        Use stack to keep track of the index of the bars
        if encounter a lower bar, keep poping the stack until the top bar in stack is smaller than the current bar
        at each index we mark the start point
        with each pop, we use the height of the popped bar and the its current index to calculate the area
        key thing is to extend the start index of the newly added bar to the final popped bar in the while loop
        this helps to keep track of the width of the overall rectangle for future bars added into the stack
        time complexity: O(n)
        space complexity: O(n)
        """
        stack = [] # (ind, height)
        maxArea = 0
		
		# popping bar whose that is higher than the current bar
        for i, height in enumerate(heights):
            start = i
            while stack and stack[-1][1] > height:
                ind, h = stack.pop()
                maxArea = max(maxArea, h*(i - ind))
                start = ind
            stack.append((start, height))
		
		# process the remaining bars left in the stack
        for i, height in stack:
            maxArea = max(maxArea, height*(len(heights) - i))

        return maxArea

Complexity

time: $O(n)$
space: $O(n)$