LC 853 - Car Fleet

Question

There are n cars at given miles away from the starting mile 0, traveling to reach the mile target.

You are given two integer arrays position and speed, both of length n, where position[i] is the starting mile of the ith car and speed[i] is the speed of the ith car in miles per hour.

A car cannot pass another car, but it can catch up and then travel next to it at the speed of the slower car.

A car fleet is a single car or a group of cars driving next to each other. The speed of the car fleet is the minimum speed of any car in the fleet.

If a car catches up to a car fleet at the mile target, it will still be considered as part of the car fleet.

Return the number of car fleets that will arrive at the destination.

Example 1:

Input: target = 12, position = [10,8,0,5,3], speed = [2,4,1,1,3]
Output: 3

Explanation:

• The cars starting at 10 (speed 2) and 8 (speed 4) become a fleet, meeting each other at 12. The fleet forms at target.
• The car starting at 0 (speed 1) does not catch up to any other car, so it is a fleet by itself.
• The cars starting at 5 (speed 1) and 3 (speed 3) become a fleet, meeting each other at 6. The fleet moves at speed 1 until it reaches target.

Example 2:

Input: `target = 10, position = [3], speed = [3]`
Output: 1

Explanation:

There is only one car, hence there is only one fleet.

Example 3:

Input: `target = 100, position = [0,2,4], speed = [4,2,1]`
Output: 1

Explanation:

• The cars starting at 0 (speed 4) and 2 (speed 2) become a fleet, meeting each other at 4. The car starting at 4 (speed 1) travels to 5.
• Then, the fleet at 4 (speed 2) and the car at position 5 (speed 1) become one fleet, meeting each other at 6. The fleet moves at speed 1 until it reaches target.

Constraints:

• n == position.length == speed.length
• 1 <= n <= 105
• 0 < target <= 106
• 0 <= position[i] < target
• All the values of position are unique.
• 0 < speed[i] <= 106

Links

Question here and solution here

Solution

concept

The main intuition is to visualize first all cars’ data on a cartesian plot. Notice that the speed is just the slope while position are the starting points which are just the y-axis. As long as there are an intersection, it means the 2 cars is going to collide at that time and space. 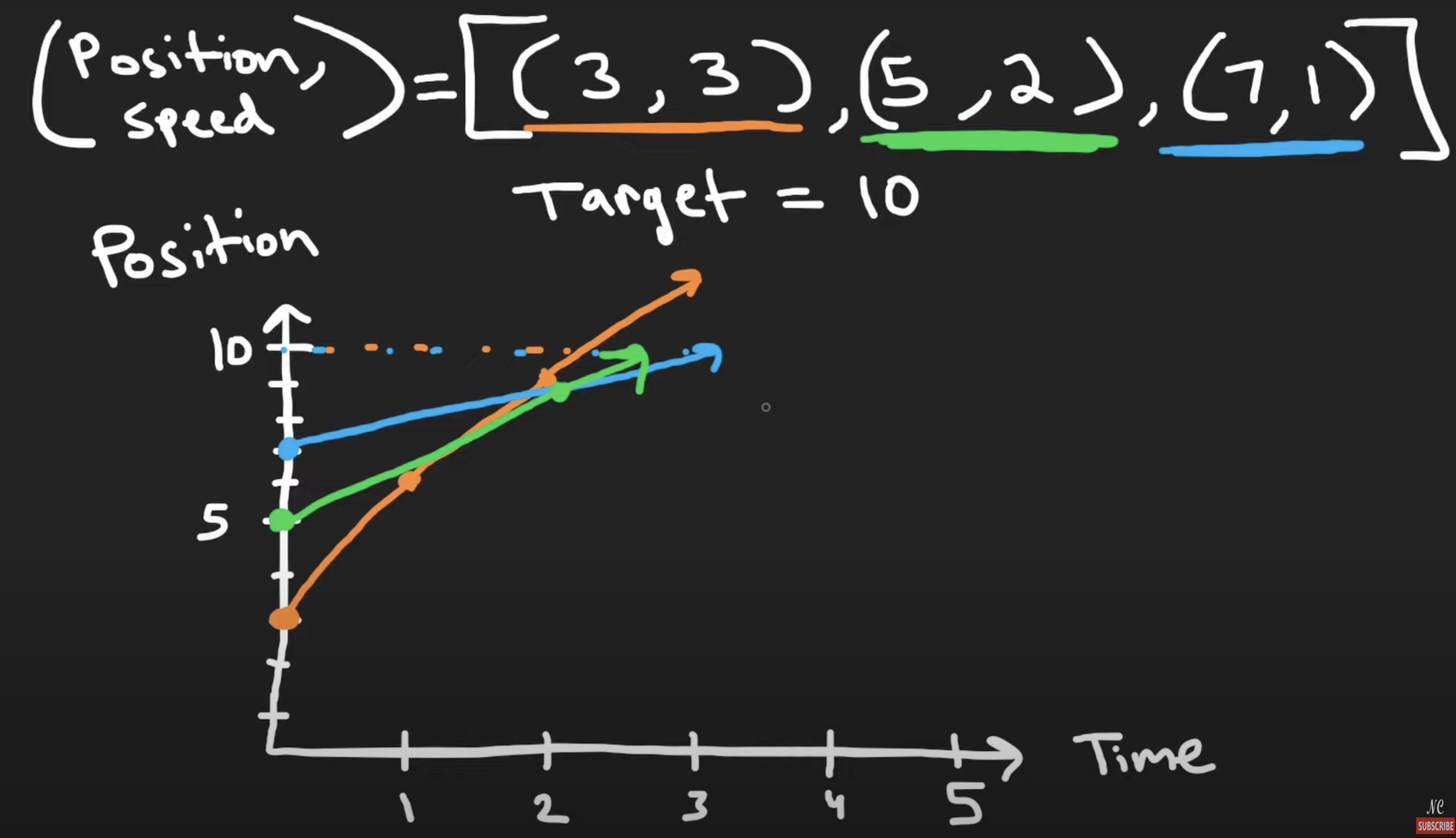To actually solve the question, we can put all the cars on the number line: 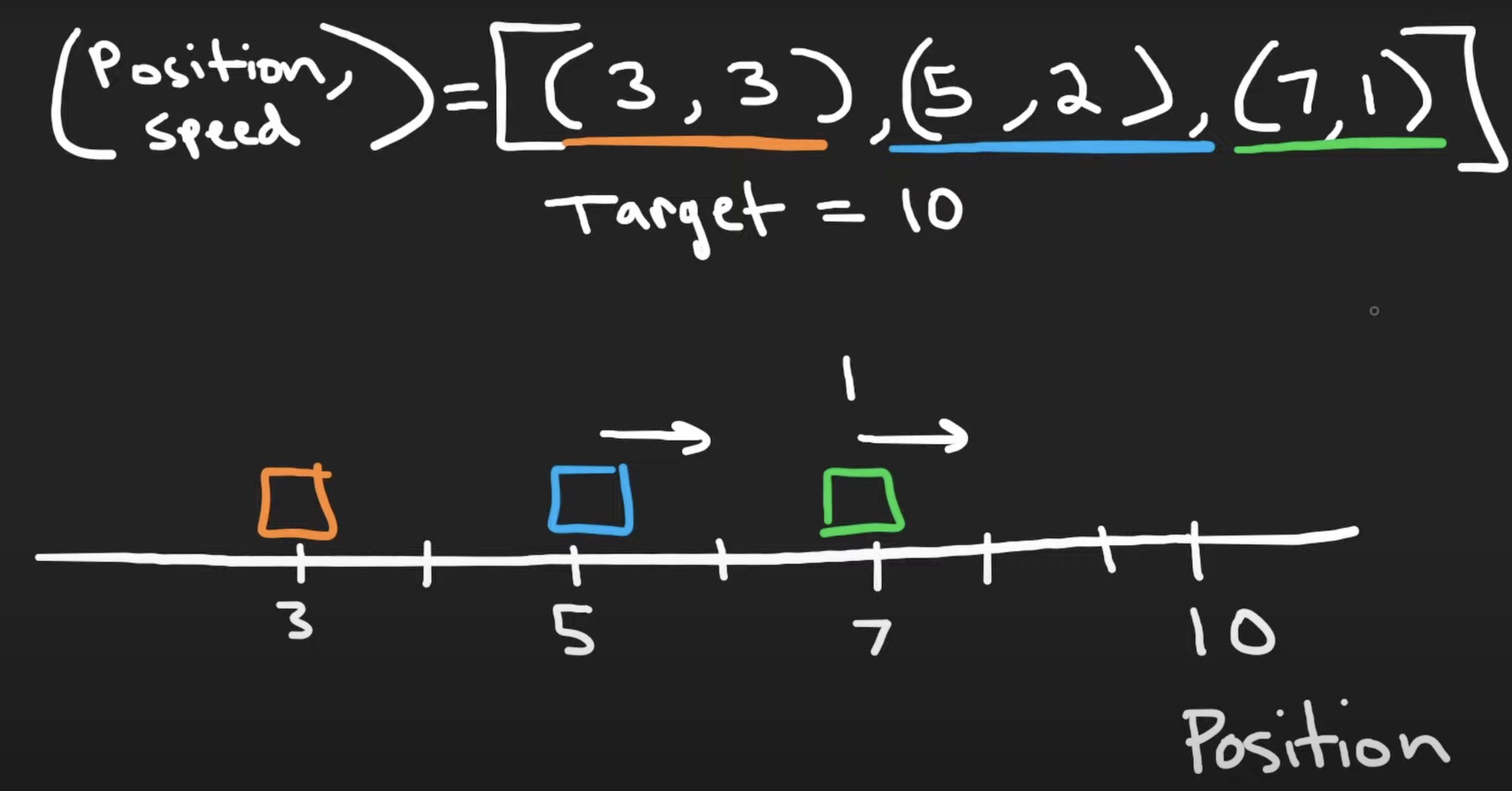There are a few observations from this:

1. we want to calculate the time for each car to reach the target, this is done by (target - position[i])/speed[i] for each car i. If the behind car has a smaller time the car in front, it means that the behind car will catch up. We can then ignore the behind car: because the behind car will be merged into the front car and since it is faster, its speed will be limited to the front car, so it is as if this behind car never existed in the number line.
2. We have to iterate from right to left in a sorted number line (by the position) since the relative order of the starting position matters, and also the target is at the right, we need to iterate from right to see which car arrives first. If we iterate from left, we do not know the front car’s speed throughout the journey, as this front car can be merged into the car ahead and reduced speed.

After sorting the data, we iterate from the right and calculate the time taken for each car to reach target. We put the time into a stack, and then compare to the adjacent time, as long as the the newly added car’s time is smaller than the previous one, it gets popped. This will results a monotonically increasing stack (since adding a smaller value gets popped)

The length of the stack is our car fleet number.

code

class Solution:
    def carFleet(self, target: int, position: List[int], speed: List[int]) -> int:
        stack = []
        pairs = [[pos, spd] for pos, spd in zip(position, speed)]

        for pos, spd in sorted(pairs)[::-1]:
            time = (target - pos) / spd
            stack.append(time)
            while len(stack) >= 2 and stack[-1] <= stack[-2]:
                stack.pop()

        return len(stack)

Complexity

time: $O(n\log n)$ : due to sorting
space: $O(n)$: need to store values in a monotonic stack