LC 90 - Subsets II

Question

Given an integer array nums that may contain duplicates, return all possible subsets (the power set).

The solution set must not contain duplicate subsets. Return the solution in any order.

Example 1:

Input: nums = [1,2,2]
Output: [[],[1],[1,2],[1,2,2],[2],[2,2]]

Example 2:

Input: nums = [0]
Output: [[],[0]]

Constraints:

• 1 <= nums.length <= 10
• -10 <= nums[i] <= 10

Links

Question here and solution here

Solution

concept

This question is very similar to 78. Subsets but it contains duplicates, but the answer still requires no duplicated subset.

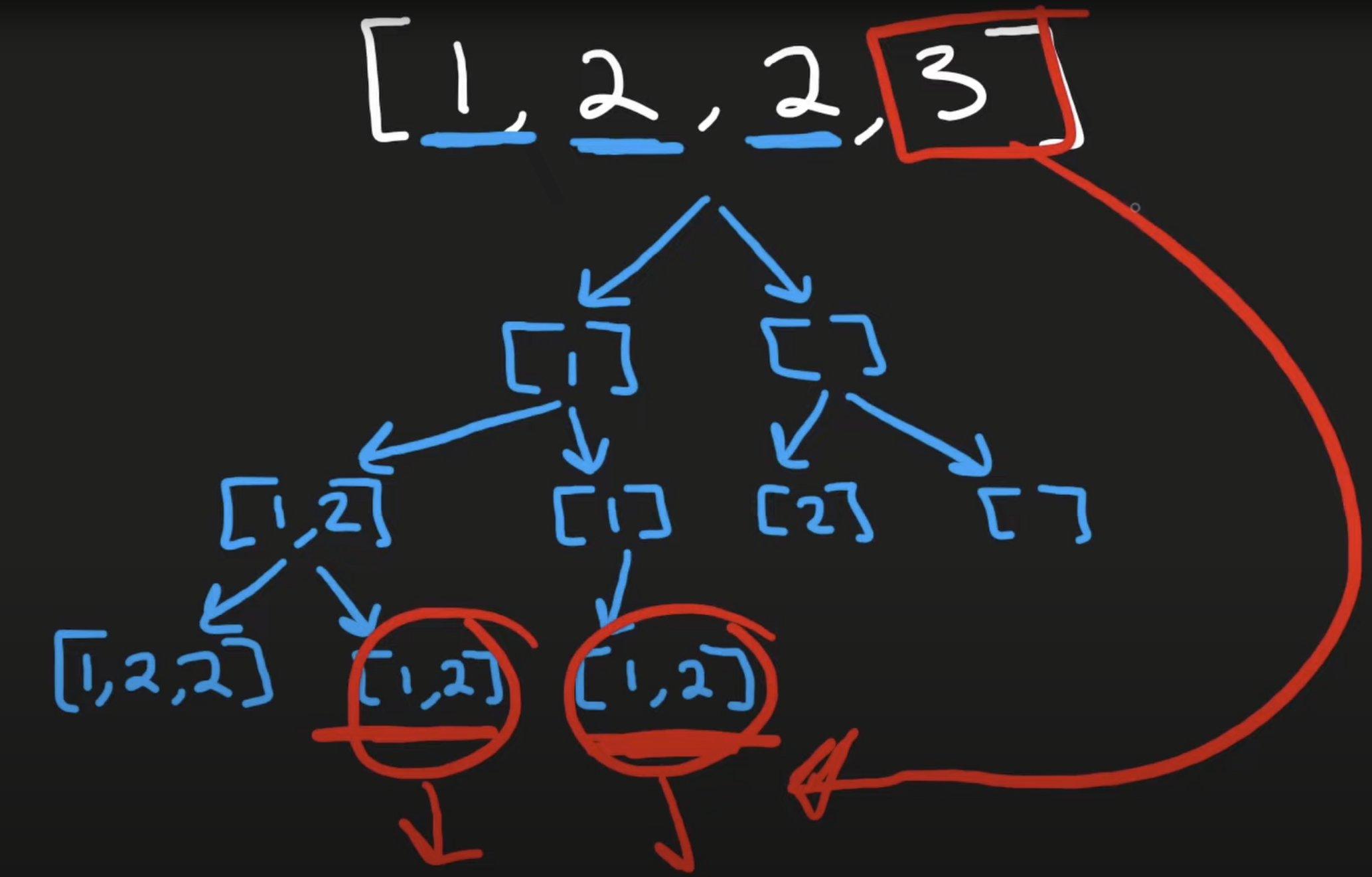
From the picture below, we see that the first branch where [1] -> [1,2] should contains all subset that contains at least one 1 and one 2 in their subsets generation down the path, this occurs includes the other branch where the 2nd 2 is being used, this means that we have to skip the duplicates when we move the index.

So this question will use the same idea of [[40. Combination Sum II]] where we first sort the input array and then use a while loop to skip duplicates

code

class Solution:
    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
        nums.sort()
        ans = []
        subset = []
        def dfs(idx):
            if idx >= len(nums):
                ans.append(subset.copy())
                return
			# include current element
			# i.e, all subsets that include the current element nums[idx]
            subset.append(nums[idx])
            dfs(idx + 1)
            subset.pop()
			# do not include current element and move to the next non-duplicated elements
			# i.e. all subsets that do not include the current element nums[idx]
            while idx < len(nums) - 1 and nums[idx] == nums[idx + 1]:
                idx += 1
            dfs(idx + 1)

        dfs(0)

        return ans
        
class Solution:
	"""
	lazy way to use set
	not that we need to sort each subset before appending to ans to reduce duplicates
	"""
    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
        ans = set()
        subset = []
        def dfs(idx):
            if idx >= len(nums):
                ans.add(tuple(sorted(subset.copy())))
                return

            subset.append(nums[idx])
            dfs(idx + 1)

            subset.pop()
            dfs(idx + 1)

        dfs(0)

        return list(ans)

Complexity

time: $O(n * 2^n)$
space: $O(2^n)$