LC 97 - Interleaving String

Question

Given strings s1, s2, and s3, find whether s3 is formed by an interleaving of s1 and s2.

An interleaving of two strings s and t is a configuration where s and t are divided into n and m substrings respectively, such that:

• s = s1 + s2 + ... + sn
• t = t1 + t2 + ... + tm
• |n - m| <= 1
• The interleaving is s1 + t1 + s2 + t2 + s3 + t3 + ... or t1 + s1 + t2 + s2 + t3 + s3 + ...

Note: a + b is the concatenation of strings a and b.

Example 1:

Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
Output: true

Explanation: One way to obtain s3 is: Split s1 into s1 = “aa” + “bc” + “c”, and s2 into s2 = “dbbc” + “a”. Interleaving the two splits, we get “aa” + “dbbc” + “bc” + “a” + “c” = “aadbbcbcac”. Since s3 can be obtained by interleaving s1 and s2, we return true.

Example 2:

Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
Output: false

Explanation: Notice how it is impossible to interleave s2 with any other string to obtain s3.

Example 3:

Input: s1 = "", s2 = "", s3 = ""
Output: true

Constraints:

• 0 <= s1.length, s2.length <= 100
• 0 <= s3.length <= 200
• s1, s2, and s3 consist of lowercase English letters.

Follow up: Could you solve it using only O(s2.length) additional memory space?

Links

Question here and solution here

Solution

concept

For the bottom up solution, we will have a 2D grid and in the grid we record down T/F which represent if we can interleave the words with the remaining s1[i:] and s2[j:] If we use the char from s1 (i.e. the y-axis) to match s3, we will check if the cell down is True, which means that with s1[i+1] and s2[j] it can interleave to form s3[i+1+j:] If we use the char from s2, then we will check the right cell if it is True. It is possible that both condition is true, i.e. both s1 and s2 match s3 at that position, then we will just update the cell to True anyway.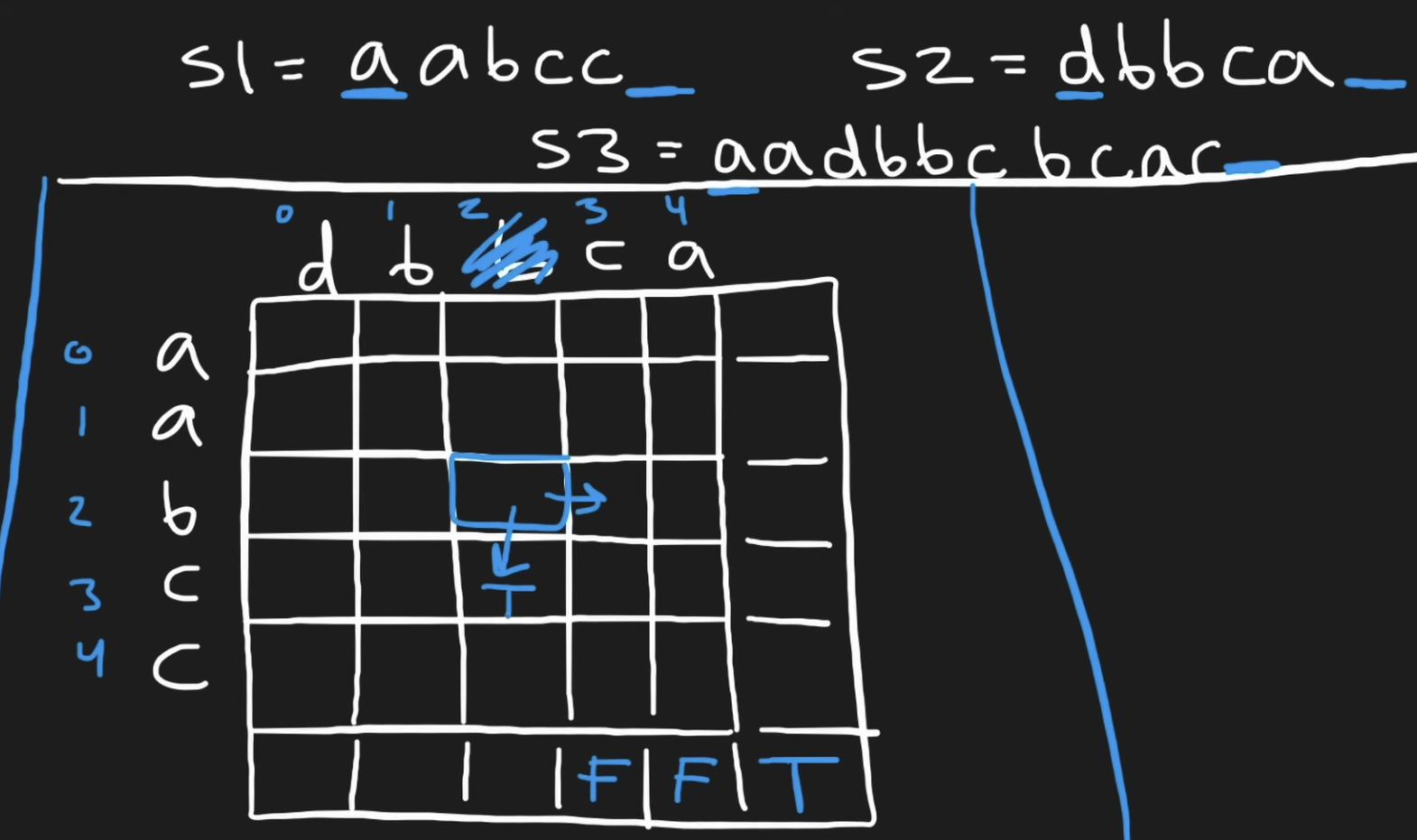

code

class Solution:
	"""
	brute force dfs
	TLE
	"""
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        
        def dfs(i,j,k):
            if k == len(s3):
                return i == len(s1) and j == len(s2)
            
            if i < len(s1) and s1[i] == s3[k]:
                if dfs(i + 1, j, k + 1):
                    return True
            
            if j < len(s2) and s2[j] == s3[k]:
                if dfs(i, j + 1, k + 1):
                    return True
            
            return False
        
        return dfs(0,0,0)

class Solution:
	"""
	top down: memoization
	"""
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        cache = {}
        def dfs(i,j,k):
            if (i,j,k) in cache:
                return cache[(i,j,k)]
            if k == len(s3):
                return i == len(s1) and j == len(s2)
            
            if i < len(s1) and s1[i] == s3[k]:
                if dfs(i + 1, j, k + 1):
                    cache[(i,j,k)] = True
                    return cache[(i,j,k)]
            
            if j < len(s2) and s2[j] == s3[k]:
                if dfs(i, j + 1, k + 1):
                    cache[(i,j,k)] = True
                    return cache[(i,j,k)]

            cache[(i,j,k)] = False
            return cache[(i,j,k)]
        
        return dfs(0,0,0)
        
class Solution:
	"""
	top down: memoization
	"""
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        if len(s1) + len(s2) != len(s3):
            return False
        cache = {}
        # i + j = k
        def dfs(i,j):
            if i == len(s1) and j == len(s2):
                return True
            if (i,j) in cache:
                return cache[(i,j)]
            
            if i < len(s1) and s1[i] == s3[i + j] and dfs(i + 1, j):
                cache[(i,j)] = True
                return cache[(i,j)]
            
            if j < len(s2) and s2[j] == s3[i + j] and dfs(i, j + 1):
                cache[(i,j)] = True
                return cache[(i,j)]

            cache[(i,j)] = False
            return cache[(i,j)]
        
        return dfs(0,0)
        
class Solution:
	"""
	bottom up solution
	"""
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        if len(s1) + len(s2) != len(s3):
            return False
        
        dp = [[False] * (len(s2) + 1) for _ in range(len(s1) + 1)]
        dp[len(s1)][len(s2)] = True

        for i in range(len(s1), -1, -1):
            for j in range(len(s2), -1, -1):
                if i < len(s1) and s1[i] == s3[i + j] and dp[i + 1][j]:
                    dp[i][j] = True
                if j < len(s2) and s2[j] == s3[i + j] and dp[i][j + 1]:
                    dp[i][j] = True

        return dp[0][0]

Complexity

time: $O(mn)$
space: $O(min(m,n))$