LC 994 - Rotting Oranges

Question

You are given an m x n grid where each cell can have one of three values:

• 0 representing an empty cell,
• 1 representing a fresh orange, or
• 2 representing a rotten orange.

Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

Example 1:

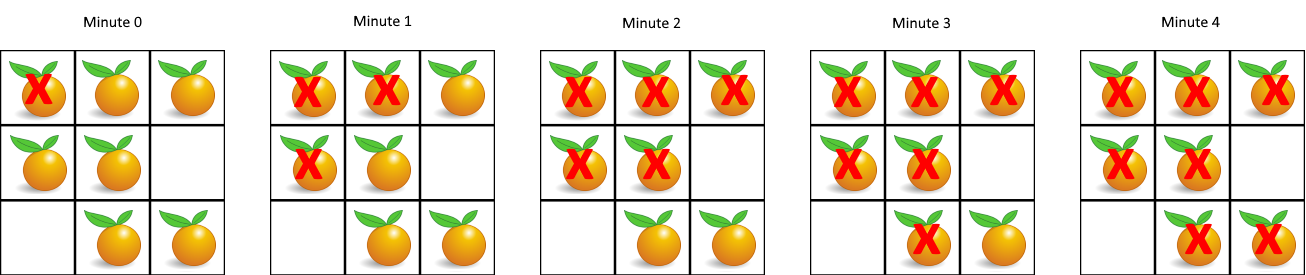
Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Example 2:

Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
Output: -1 **Explanation:** The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Example 3:

Input: grid = [[0,2]]
Output: 0 **Explanation:** Since there are already no fresh oranges at minute 0, the answer is just 0.

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 10
• grid[i][j] is 0, 1, or 2.

Links

Question here and solution here

Solution

concept

This question is very similar to [[286. Walls and Gates]] where we need to do multi-source BFS starting from the rotten orange. We need to keep track the number of fresh orange since it is possible that some of the fresh orange is not connected to the rotten ones so the answer might be -1. Note that we use fresh orange in the while loop condition and it will terminate once the there is no fresh orange, so it will not be execute extra step += 1.

Note that in [[286. Walls and Gates]] where we might have an extra step at the end but we are not updating the board so this extra +1 value is not being shown in the final answer. But here if we do not track fresh the answer might show this extra +1.

code

class Solution:
    def orangesRotting(self, grid: List[List[int]]) -> int:
        ROWS, COLS = len(grid), len(grid[0])
        step = 0
        q = deque()
        directions = [[0,1], [1,0], [0,-1], [-1,0]]
 
        fresh = 0
        for r in range(ROWS):
            for c in range(COLS):
                if grid[r][c] == 2:
                    q.append((r,c))
                if grid[r][c] == 1:
                    fresh += 1

        while fresh > 0 and q:
            for _ in range(len(q)):
                r, c = q.popleft()
                for dr, dc in directions:
                    n_r, n_c = r + dr, c + dc
                    if (0 <= n_r < ROWS and
                        0 <= n_c < COLS and
                        grid[n_r][n_c] == 1):
                        grid[n_r][n_c] = 2
                        fresh -= 1
                        q.append((n_r,n_c))
            step += 1

        return step if fresh == 0 else -1

Complexity

time: $O(mn)$
space: $O(mn)$